Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T04:59:46.139Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Borel-Cantelli Problem

Published online by Cambridge University Press:  20 November 2018

Jonathan Shuster
Jonathan Shuster*
Affiliation:
McGill University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (Ω, 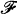, P) be a probability space, and A 1, A 2… be a sequence of members of 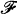. The classical Borel-Cantelli problem is to determine the probability that infinitely many events A k occur. The classical results may be found in Feller [2, p. 188]; while related work may be found in Spitzer [3, p. 317], and Dawson and Sankoff [1]. The latter works are generalizations of the Borel-Cantelli lemmas, taken in different directions.

In this paper, necessary and sufficient conditions will be given for infinitely many events A k to occur, with probability 1. A lower bound for the probability that only finitely many A k occur, is developed. In addition, necessary and sufficient conditions that only finitely many A k occur, with probability 1, are given.

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 2 , June 1970 , pp. 273 - 275
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Dawson, D. and Sankoff, D., An inequality for probabilities, Proc. Amer. Math. Soc. (3) 18 (1967), 504-507.Google Scholar
2. Feller, W., An introduction to probability theory and its applications, Wiley, New York, I (second edition), 1957.Google Scholar
3. Spitzer, F., Principles of random walk, Van Nostrand, Princeton, N.J., 1964.Google Scholar