No CrossRef data available.
Article contents
On s-semipermutable or s-quasinormally Embedded Subgroups of Finite Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
Suppose that  $G$ is a finite group and
$G$ is a finite group and 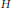 $H$ is a subgroup of
$H$ is a subgroup of  $G$ .
$G$ . 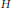 $H$ is said to be
$H$ is said to be  $s$ -semipermutable in
$s$ -semipermutable in  $G$ if
$G$ if 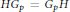 $H{{G}_{p}}\,=\,{{G}_{p}}H$ for any Sylow
$H{{G}_{p}}\,=\,{{G}_{p}}H$ for any Sylow  $p$ -subgroup
$p$ -subgroup 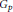 ${{G}_{p}}$ of
${{G}_{p}}$ of  $G$ with
$G$ with 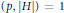 $\left( p,\,\left| H \right| \right)\,=\,1$ ;
$\left( p,\,\left| H \right| \right)\,=\,1$ ;  $H$ is said to be
$H$ is said to be  $s$ -quasinormally embedded in
$s$ -quasinormally embedded in  $G$ if for each prime
$G$ if for each prime  $p$ dividing the order of
$p$ dividing the order of  $H$ , a Sylow
$H$ , a Sylow  $p$ -subgroup of
$p$ -subgroup of  $H$ is also a Sylow
$H$ is also a Sylow  $p$ -subgroup of some
$p$ -subgroup of some  $s$ -quasinormal subgroup of
$s$ -quasinormal subgroup of  $G$ . In every non-cyclic Sylow subgroup
$G$ . In every non-cyclic Sylow subgroup 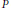 $P$ of
$P$ of  $G$ we fix some subgroup
$G$ we fix some subgroup 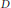 $D$ satisfying
$D$ satisfying 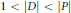 $1\,<\,\left| D \right|\,<\,\left| P \right|$ and study the structure of
$1\,<\,\left| D \right|\,<\,\left| P \right|$ and study the structure of  $G$ under the assumption that every subgroup
$G$ under the assumption that every subgroup 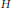 $H$ of
$H$ of 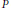 $P$ with
$P$ with 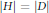 $\left| H \right|\,=\,\left| D \right|$ is either
$\left| H \right|\,=\,\left| D \right|$ is either  $s$ -semipermutable or
$s$ -semipermutable or  $s$ -quasinormally embedded in
$s$ -quasinormally embedded in  $G$ . Some recent results are generalized and unified.
$G$ . Some recent results are generalized and unified.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015

