Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
El-Bast, Zeinab Abd
and
Smith, Patrick P.
1988.
Multiplication modules.
Communications in Algebra,
Vol. 16,
Issue. 4,
p.
755.
McCasland, R. L.
and
Moore, M. E.
1991.
On radicals of submodules.
Communications in Algebra,
Vol. 19,
Issue. 5,
p.
1327.
McCasland, R.L.
and
Moore, M.E.
1992.
Prime submodules.
Communications in Algebra,
Vol. 20,
Issue. 6,
p.
1803.
Jenkins, James
and
Smith, Patrick F.
1992.
On the prime radical of a module over a commutative ring.
Communications in Algebra,
Vol. 20,
Issue. 12,
p.
3593.
Man, Shing Hing
1996.
One dimensional domains which satisfy the radical formula are Dedekind domains.
Archiv der Mathematik,
Vol. 66,
Issue. 4,
p.
276.
Leung, Ka Hin
and
Man, Shing Hing
1997.
On commutative Noetherian rings which satisfy the radical formula.
Glasgow Mathematical Journal,
Vol. 39,
Issue. 3,
p.
285.
Marcelo, Agustín
Marcelo, Félix
and
Rodríguez, César
1999.
Computer Algebra in Scientific Computing CASC’99.
p.
287.
Marcelo, Agustín
and
Rodríguez, César
2000.
Radical of submodules and symmetric algebra.
Communications in Algebra,
Vol. 28,
Issue. 10,
p.
4611.
Tiras, Yücel
and
Harmanci, Abdullah
2000.
On prime submodules and primary decomposition.
Czechoslovak Mathematical Journal,
Vol. 50,
Issue. 1,
p.
83.
Tiraş, Yücel
and
Alkan, Mustafa
2003.
Prime Modules and Submodules.
Communications in Algebra,
Vol. 31,
Issue. 11,
p.
5253.
Divaani-aazar, Kamran
and
Esmkhani, Mohammad Ali
2005.
Associated Prime Submodules of Finitely Generated Modules.
Communications in Algebra,
Vol. 33,
Issue. 11,
p.
4259.
Alkan, Mustafa
and
Tiraş, Yücel
2006.
Projective modules and prime submodules.
Czechoslovak Mathematical Journal,
Vol. 56,
Issue. 2,
p.
601.
Tekir, Ünsal
2006.
A Note on Dedekind and ZPI Modules.
Algebra Colloquium,
Vol. 13,
Issue. 01,
p.
41.
Ali, Majid M.
2008.
Idempotent and Nilpotent Submodules of Multiplication Modules.
Communications in Algebra,
Vol. 36,
Issue. 12,
p.
4620.
Samei, Karim
2008.
On the Maximal Spectrum of Semiprimitive Multiplication Modules.
Canadian Mathematical Bulletin,
Vol. 51,
Issue. 3,
p.
439.
Lu, Chin-Pi
2010.
Modules with Noetherian Spectrum.
Communications in Algebra,
Vol. 38,
Issue. 3,
p.
807.
SAMEI, KARIM
2011.
Reduced multiplication modules.
Proceedings - Mathematical Sciences,
Vol. 121,
Issue. 2,
p.
121.
NIKSERESHT, A.
and
AZIZI, A.
2011.
ON RADICAL FORMULA IN MODULES.
Glasgow Mathematical Journal,
Vol. 53,
Issue. 3,
p.
657.
ZAMANI, NASER
2011.
FINITELY GENERATED GRADED MULTIPLICATION MODULES.
Glasgow Mathematical Journal,
Vol. 53,
Issue. 3,
p.
693.
RUSH, DAVID E.
2011.
NOETHERIAN SPECTRUM ON RINGS AND MODULES.
Glasgow Mathematical Journal,
Vol. 53,
Issue. 3,
p.
707.

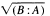 denotes the ideal radical of (B:A), then M-rad
denotes the ideal radical of (B:A), then M-rad 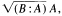 provided that A is a finitely generated multiplication module. Additionally, it is shown that if A is an arbitrary module,
provided that A is a finitely generated multiplication module. Additionally, it is shown that if A is an arbitrary module, 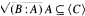
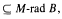 where
where 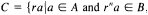 for some
for some