No CrossRef data available.
Article contents
On Homogeneous Expansions of Mixed Norm Space Functions in the Ball
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For f analytic in the complex ball having the homogeneous expansion 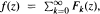 conditions for f to be of Hardy space Hp or of weighted Bergman spaces are expressed in terms of lp properties of the sequence {∥Fk∥p}.
conditions for f to be of Hardy space Hp or of weighted Bergman spaces are expressed in terms of lp properties of the sequence {∥Fk∥p}.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1993
References
1.
Ahern, P. and Bruna, J., Maximal and area characterization of Hardy-Sobolev spaces in the unit ball of Cn, Revista Mathemätica Iberoamericana 4( 1988), 123–153.Google Scholar
2.
Ahern, P. and Bruna, J., On the holomorphicfunctions in the ball with absolutely continuous boundary values, Duke Math. J., to appearGoogle Scholar
3.
Ahem, P. and W Rudin, Bloch functions, BMO, and boundary zeros, Indiana Univ. Math. J. 36(1987), 131–148.Google Scholar
4.
Ahem, P. and W Rudin, Paley type gap theorems for Hp functions on the ball, Indiana Univ. Math. J. 37(1988), 255–275.Google Scholar
5.
Alexander, H., Projective Capacity, Recent Developments in Several Complex Variables, Annals of Math. Studio 100,1981
Google Scholar
6.
Beatrous, F. and Burbea, J., Holomorphic Sobolev spaces in the ball, Dissertationes Math. 276(1989), 1–57.Google Scholar
8.
Hardy, G. H. and Littlewood, J. E., Theorems concerning mean values of analytic functions or harmonic functions, Quart J. Math. Oxford Ser. 12(1941), 221–256.Google Scholar
9.
Kellog, C. N., An extension of the Hausdorff-Young Theorem, Michigan Math. J. 8(1971), 121–127.Google Scholar
10.
Kwak, Do Young, Hardy-Littlewood inequalities for weighted Bergman spaces, Communications of the Korean Mathematical Society 2(1987), 33–37.Google Scholar
11.
Kwon, E. G., A note on the Taylor coefficients of mixed normed spaces, Bull. Austral. Math. Soc. 33(1986), 253–260.Google Scholar
12.
Mateljevic’, M. and Pavlovic', M., LP -behavior of power series with positive coefficients and Hardy spaces, Proc. Amer. Math. Soc. 87(1983), 309–316.Google Scholar
13.
Paley, R. E. A. C., On the lacunary coefficients of power series, Ann of Math 34(1933), 615–616.Google Scholar
14.
Rudin, W., Function theory in the unit ball of Cn
, Springer-Verlag, New York, 1980
Google Scholar
15.
Rudin, W., New constructions of functions holomorphic in the unit ball of Cn
, Conference Board of the Mathematical Science by AMS, 1985
Google Scholar
16.
Ryll, J. and Wojtaszczyk, P., On homogeneous polynomials on a complex ball, Trans. Amer. Math. Soc. 276(1983),107–116.Google Scholar

