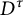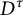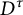1 Introduction
Knaster and Reichbach [Reference Knaster and Reichbach5] established the following theorem, which is considered as a classical result (see also [Reference Pollard10] for other types of zero-dimensional separable metric spaces where similar results hold): Let X and Y be compact, perfect zero-dimensional metric spaces, and let P and K be closed nowhere dense subsets of X and Y, respectively. If f is a homeomorphism between P and K, then there exists a homeomorphism between X and Y extending f.
If we omit the metrizability condition in Knaster–Reichbach’s theorem, then the conclusion is not anymore true. In order to obtain a correct generalization of the theorem, first of all, it is necessary to find the correct analogue of the condition “nowhere dense.” Moreover, the perfectness condition can be formulated as the nowhere density of the points.
Such an analogue is the following concept of negligibility. A subset of a topological space is called negligible if it does not contain a nonempty intersection of a family of open sets such that the cardinality of the family is less than the weight of the space. Note that for metric compacta, the condition of nowhere density is equivalent to the condition of negligibility.
Now we are able to provide a generalization of Knaster–Reichbach’s theorem.
Theorem 1.1 Let X and Y be compact, zero-dimensional absolute extensors for zero-dimensional spaces of the same weight with negligible points, and let P and K be closed negligible subsets of X and Y, respectively. If f is a homeomorphism between P and K, then there exists a homeomorphism between X and Y extending f.
This theorem for metric compacta turns into Knaster–Reichbach’s theorem because every metric compact space is an absolute extensor in dimension 0. In general, it is very difficult to avoid the condition of being an absolute extensor in dimension 0 because extending of homeomorphisms is based on the extension of continuous maps.
Since the negligibility of a point in a compactum is equivalent to having a character at that point equal to the weight of the compactum, Theorem 1 from [Reference Shchepin11] allows us to assert that the compacta X and Y in Theorem 1.1 are homeomorphic to the Cantor cube
![]() $D^{\tau }$
, where
$D^{\tau }$
, where
![]() $\tau $
is the weight of X and Y. Therefore, the above theorem can be obtained from the following special case of its own.
$\tau $
is the weight of X and Y. Therefore, the above theorem can be obtained from the following special case of its own.
Theorem 1.2 Let f be a homeomorphism between closed negligible subsets P and K of
![]() $D^{\tau }$
. Then f can be extended to a homeomorphism of
$D^{\tau }$
. Then f can be extended to a homeomorphism of
![]() $D^{\tau }$
.
$D^{\tau }$
.
Since every subset of
![]() $D^{\tau }$
having weight less than
$D^{\tau }$
having weight less than
![]() $\tau $
is negligible, we have the following corollary.
$\tau $
is negligible, we have the following corollary.
Corollary 1.3 If
![]() $P,K$
are closed subsets of
$P,K$
are closed subsets of
![]() $D^{\tau }$
both of weight
$D^{\tau }$
both of weight
![]() $<\tau $
, then every homeomorphism between P and K can be extended to homeomorphism of
$<\tau $
, then every homeomorphism between P and K can be extended to homeomorphism of
![]() $D^{\tau }$
.
$D^{\tau }$
.
Similar results for extending homeomorphisms between subsets of the Tychonoff cube
![]() $\mathbb I^{\tau }$
were established by Chigogidze [Reference Chigogidze2, Corollary 4.10] and Mednikov [Reference Mednikov7]. Our result is simpler and does not follow from them. Our proof is based on Michael’s zero-dimensional selection theorem [Reference Michael9].
$\mathbb I^{\tau }$
were established by Chigogidze [Reference Chigogidze2, Corollary 4.10] and Mednikov [Reference Mednikov7]. Our result is simpler and does not follow from them. Our proof is based on Michael’s zero-dimensional selection theorem [Reference Michael9].
2 Some preliminary results
Anywhere below, by a homeomorphism, we always mean a surjective homeomorphism. We need a more precise notion of negligibility. For a space X, a subset
![]() $P\subset X$
, and an infinite cardinal
$P\subset X$
, and an infinite cardinal
![]() $\lambda $
, we denote by
$\lambda $
, we denote by
![]() $P^{(\lambda )}$
the
$P^{(\lambda )}$
the
![]() $\lambda $
-interior of P in X, i.e., the set all
$\lambda $
-interior of P in X, i.e., the set all
![]() $x\in P$
such that there exists a
$x\in P$
such that there exists a
![]() $G_{\lambda }$
-subset K of X with
$G_{\lambda }$
-subset K of X with
![]() $x\in K\subset P$
. If
$x\in K\subset P$
. If
![]() $\lambda $
is finite, then
$\lambda $
is finite, then
![]() $P^{(\lambda )}$
is defined to be the ordinary interior of P and it is denoted by
$P^{(\lambda )}$
is defined to be the ordinary interior of P and it is denoted by
![]() $P^{(0)}$
. If there exists
$P^{(0)}$
. If there exists
![]() $\tau \geq \aleph _0$
such that
$\tau \geq \aleph _0$
such that
![]() $P^{(\lambda )}$
is empty for all
$P^{(\lambda )}$
is empty for all
![]() $\lambda <\tau $
, we say that P is
$\lambda <\tau $
, we say that P is
![]() $\tau $
-negligible in X. Let
$\tau $
-negligible in X. Let
![]() $X=\prod _{\alpha \in A}X_{\alpha }$
be a product of spaces and
$X=\prod _{\alpha \in A}X_{\alpha }$
be a product of spaces and
![]() $B\subset A$
. If
$B\subset A$
. If
![]() $P\subset X$
, then
$P\subset X$
, then
![]() $P_B$
denotes
$P_B$
denotes
![]() $\pi _B(P)$
, where
$\pi _B(P)$
, where
![]() $\pi _B:X\to \prod _{\alpha \in B}X_{\alpha }$
is the projection.
$\pi _B:X\to \prod _{\alpha \in B}X_{\alpha }$
is the projection.
Proposition 2.1 Let
![]() $X=\prod _{\alpha \in A}X_{\alpha }$
be a product of separable metric spaces, let P be a compact subset of X, and let
$X=\prod _{\alpha \in A}X_{\alpha }$
be a product of separable metric spaces, let P be a compact subset of X, and let
![]() $f:P\to P$
be a homeomorphism. Then, for any countable set
$f:P\to P$
be a homeomorphism. Then, for any countable set
![]() $C\subset A$
, there are a countable set
$C\subset A$
, there are a countable set
![]() $B\subset A$
and a homeomorphism
$B\subset A$
and a homeomorphism
![]() $f_B:P_B\to P_B$
such that
$f_B:P_B\to P_B$
such that
![]() $C\subset B$
and
$C\subset B$
and
![]() $\pi _B\circ f=f_B\circ \pi _B$
.
$\pi _B\circ f=f_B\circ \pi _B$
.
Proof Obviously, this is true for a countable set A, so we suppose that A is uncountable. Let
![]() $f^{-1}$
be the inverse of f. Using that P is C-embedded in X and any continuous function on X depends on countably many coordinates (see [Reference Engelking3, Reference Mibu8]), we construct by induction sequences of countable sets
$f^{-1}$
be the inverse of f. Using that P is C-embedded in X and any continuous function on X depends on countably many coordinates (see [Reference Engelking3, Reference Mibu8]), we construct by induction sequences of countable sets
![]() $B(n)\subset A$
and maps
$B(n)\subset A$
and maps
![]() $f_{B(2n-1)}:P_{B(2n)}\to P_{B(2n-1)}$
and
$f_{B(2n-1)}:P_{B(2n)}\to P_{B(2n-1)}$
and
![]() $g_{B(2n)}:P_{B(2n+1)}\to P_{B(2n)}$
such that:
$g_{B(2n)}:P_{B(2n+1)}\to P_{B(2n)}$
such that:
-
•
 $B(1)=C$
,
$B(1)=C$
,
 $B(n)\subset B(n+1)$
.
$B(n)\subset B(n+1)$
. -
•
 $\displaystyle \pi _{B(2n-1)}\circ f=f_{B(2n-1)}\circ \pi _{B(2n)}$
.
$\displaystyle \pi _{B(2n-1)}\circ f=f_{B(2n-1)}\circ \pi _{B(2n)}$
. -
•
 $\displaystyle \pi _{B(2n)}\circ f^{-1}=g_{B(2n)}\circ \pi _{B(2n+1)}$
.
$\displaystyle \pi _{B(2n)}\circ f^{-1}=g_{B(2n)}\circ \pi _{B(2n+1)}$
.
Then
![]() $B=\bigcup _{n=1}^{\infty } B(n)$
is countable and the equality
$B=\bigcup _{n=1}^{\infty } B(n)$
is countable and the equality
![]() $\pi _B(x)=\pi _B(y)$
implies
$\pi _B(x)=\pi _B(y)$
implies
![]() $\pi _B(f(x))=\pi _B(f(y))$
and
$\pi _B(f(x))=\pi _B(f(y))$
and
![]() $\pi _B(f^{-1}(x))=\pi _B(f^{-1}(y))$
for all
$\pi _B(f^{-1}(x))=\pi _B(f^{-1}(y))$
for all
![]() $x,y\in P$
. Since
$x,y\in P$
. Since
![]() $P_B$
is compact, there exist maps
$P_B$
is compact, there exist maps
![]() $f_B:P_B\to P_B$
and
$f_B:P_B\to P_B$
and
![]() $g_B:P_B\to P_B$
with
$g_B:P_B\to P_B$
with
![]() $\displaystyle \pi _B\circ f=f_B\circ \pi _B$
,
$\displaystyle \pi _B\circ f=f_B\circ \pi _B$
,
![]() $\displaystyle \pi _B\circ f^{-1}=g_B\circ \pi _B$
, and
$\displaystyle \pi _B\circ f^{-1}=g_B\circ \pi _B$
, and
![]() $f_B\circ g_B$
is the identity on
$f_B\circ g_B$
is the identity on
![]() $P_B$
. Then
$P_B$
. Then
![]() $f_B$
is an autohomeomorphism of
$f_B$
is an autohomeomorphism of
![]() $P_B$
.
$P_B$
.
In the situation of Proposition 2.1, a subset
![]() $B\subset A$
is called f-admissible if there exists a homeomorphism
$B\subset A$
is called f-admissible if there exists a homeomorphism
![]() $f_B:P_B\to P_B$
with
$f_B:P_B\to P_B$
with
![]() $\displaystyle \pi _{B}\circ f=f_B\circ \pi _{B}$
. It is easily seen that arbitrary union of f-admissible sets is also f-admissible.
$\displaystyle \pi _{B}\circ f=f_B\circ \pi _{B}$
. It is easily seen that arbitrary union of f-admissible sets is also f-admissible.
In [Reference Mednikov6],
![]() $\tau $
-negligible sets with
$\tau $
-negligible sets with
![]() $\tau>\aleph _0$
were considered under the name
$\tau>\aleph _0$
were considered under the name
![]() $\widetilde {G}_{\tau }$
-sets. By [Reference Mednikov6, Lemma 6], if X is a product of metric compacta and
$\widetilde {G}_{\tau }$
-sets. By [Reference Mednikov6, Lemma 6], if X is a product of metric compacta and
![]() $\tau>\aleph _0$
, then a closed set
$\tau>\aleph _0$
, then a closed set
![]() $F\subset X$
is
$F\subset X$
is
![]() $\tau $
-negligible in X if and only if the
$\tau $
-negligible in X if and only if the
![]() $\pi $
-character
$\pi $
-character
![]() $\pi \chi (F,X)$
of F in X is
$\pi \chi (F,X)$
of F in X is
![]() ${\geq}{\tau} $
. Recall that
${\geq}{\tau} $
. Recall that
![]() $\pi \chi (F,X)$
is the smallest cardinality
$\pi \chi (F,X)$
is the smallest cardinality
![]() $\lambda $
such that there is an open family
$\lambda $
such that there is an open family
![]() $\mathcal U$
in X of cardinality
$\mathcal U$
in X of cardinality
![]() $\lambda $
with the following property: Every neighborhood of F in X contains an element of
$\lambda $
with the following property: Every neighborhood of F in X contains an element of
![]() $\mathcal U$
.
$\mathcal U$
.
The next lemma is a modification of [Reference Mednikov6, Theorem 2].
Lemma 2.2 Let
![]() $X=\prod _{\alpha \in A}X_{\alpha }$
be a product of compact metric spaces, and let P be a closed set in X. Suppose that
$X=\prod _{\alpha \in A}X_{\alpha }$
be a product of compact metric spaces, and let P be a closed set in X. Suppose that
![]() $\tau>\aleph _0$
and
$\tau>\aleph _0$
and
![]() $C\subset A$
is a set of cardinality
$C\subset A$
is a set of cardinality
![]() $<\tau $
such that
$<\tau $
such that
![]() $(\{z\}\times X_{A\backslash C})\cap P$
is
$(\{z\}\times X_{A\backslash C})\cap P$
is
![]() $\tau $
-negligible in
$\tau $
-negligible in
![]() $\{z\}\times X_{A\backslash C}$
for every
$\{z\}\times X_{A\backslash C}$
for every
![]() $z\in P_C$
. Then
$z\in P_C$
. Then
![]() $P_{A\backslash C}\neq X_{A\backslash C}$
.
$P_{A\backslash C}\neq X_{A\backslash C}$
.
Proof Since
![]() $(\{z\}\times X_{A\backslash C})\cap P$
is
$(\{z\}\times X_{A\backslash C})\cap P$
is
![]() $\tau $
-negligible in
$\tau $
-negligible in
![]() $\{z\}\times X_{A\backslash C}$
for every
$\{z\}\times X_{A\backslash C}$
for every
![]() $z\in P_C$
, the cardinality of
$z\in P_C$
, the cardinality of
![]() $A\backslash C$
is at least
$A\backslash C$
is at least
![]() $\tau $
. Suppose that
$\tau $
. Suppose that
![]() $P_{A\backslash C}=X_{A\backslash C}$
. Passing to a subset of P, we may assume that the projection
$P_{A\backslash C}=X_{A\backslash C}$
. Passing to a subset of P, we may assume that the projection
![]() $\pi _{A\backslash C}$
restricted to P is an irreducible map onto
$\pi _{A\backslash C}$
restricted to P is an irreducible map onto
![]() $X_{A\backslash C}$
. Denote this map by f and fix
$X_{A\backslash C}$
. Denote this map by f and fix
![]() $z\in P_C$
. Because f is irreducible, we have
$z\in P_C$
. Because f is irreducible, we have
On the other hand,
![]() $\pi \chi ((\{z\}\times X_{A\backslash C})\cap P,P)\leq \pi \chi (z,P_C)<\tau $
. So,
$\pi \chi ((\{z\}\times X_{A\backslash C})\cap P,P)\leq \pi \chi (z,P_C)<\tau $
. So,
![]() $\pi \chi (f((\{z\}\times X_{A\backslash C})\cap P),X_{A\backslash C})<\tau $
. This, according to [Reference Mednikov6, Lemma 6], means that
$\pi \chi (f((\{z\}\times X_{A\backslash C})\cap P),X_{A\backslash C})<\tau $
. This, according to [Reference Mednikov6, Lemma 6], means that
![]() $f((\{z\}\times X_{A\backslash C})\cap P)$
is not
$f((\{z\}\times X_{A\backslash C})\cap P)$
is not
![]() $\tau $
-negligible in
$\tau $
-negligible in
![]() $X_{A\backslash C}$
. Since
$X_{A\backslash C}$
. Since
![]() $f((\{z\}\times X_{A\backslash C})\cap P)$
is homeomorphic to
$f((\{z\}\times X_{A\backslash C})\cap P)$
is homeomorphic to
![]() $(\{z\}\times X_{A\backslash C})\cap P$
and
$(\{z\}\times X_{A\backslash C})\cap P$
and
![]() $X_{A\backslash C}$
is homeomorphic to
$X_{A\backslash C}$
is homeomorphic to
![]() $\{z\}\times X_{A\backslash C}$
,
$\{z\}\times X_{A\backslash C}$
,
![]() $(\{z\}\times X_{A\backslash C})\cap P$
is not
$(\{z\}\times X_{A\backslash C})\cap P$
is not
![]() $\tau $
-negligible in
$\tau $
-negligible in
![]() $\{z\}\times X_{A\backslash C}$
, a contradiction.
$\{z\}\times X_{A\backslash C}$
, a contradiction.
Let us note that the condition
![]() $\tau>\aleph _0$
in Lemma 2.2 is essential. The following example was provided by van Mill [Reference van Mill12]: Let
$\tau>\aleph _0$
in Lemma 2.2 is essential. The following example was provided by van Mill [Reference van Mill12]: Let
![]() $X=\prod _{n=0}^{\infty } X_n$
with
$X=\prod _{n=0}^{\infty } X_n$
with
![]() $X_n=[0,1]$
for every n,
$X_n=[0,1]$
for every n,
![]() $C=\{0\}$
, and let
$C=\{0\}$
, and let
![]() $f:X_0\to X_{A\backslash C}=\prod _{n=1}^{\infty } X_n$
be a continuous surjection. Then the graph
$f:X_0\to X_{A\backslash C}=\prod _{n=1}^{\infty } X_n$
be a continuous surjection. Then the graph
![]() $G(f)$
of f meets every vertical slice in a single point and hence is negligible, but
$G(f)$
of f meets every vertical slice in a single point and hence is negligible, but
![]() $\pi _{A\backslash C}(G(f))=X_{A\backslash C}$
.
$\pi _{A\backslash C}(G(f))=X_{A\backslash C}$
.
Proposition 2.3 Let
![]() $X=\prod _{\alpha \in A}X_{\alpha }$
be a product of compact metric spaces, and let P be a closed
$X=\prod _{\alpha \in A}X_{\alpha }$
be a product of compact metric spaces, and let P be a closed
![]() $\tau $
-negligible set in X with
$\tau $
-negligible set in X with
![]() $\tau>\aleph _0$
. If
$\tau>\aleph _0$
. If
![]() $C\subset A$
is a set of cardinality
$C\subset A$
is a set of cardinality
![]() $<\tau $
, then there is a set
$<\tau $
, then there is a set
![]() $B\subset A$
containing C such that
$B\subset A$
containing C such that
![]() $B\backslash C$
is countable and
$B\backslash C$
is countable and
![]() $P_{B\backslash C}$
is nowhere dense in
$P_{B\backslash C}$
is nowhere dense in
![]() $X_{B\backslash C}$
. If, in addition,
$X_{B\backslash C}$
. If, in addition,
![]() $f:P\to P$
is a homeomorphism and C is f-admissible, then we can assume that B is also f-admissible.
$f:P\to P$
is a homeomorphism and C is f-admissible, then we can assume that B is also f-admissible.
Proof Let
![]() $\Gamma \subset A$
be a set of cardinality
$\Gamma \subset A$
be a set of cardinality
![]() $<\tau $
. Since P is a
$<\tau $
. Since P is a
![]() $\tau $
-negligible set in X, so are the sets
$\tau $
-negligible set in X, so are the sets
![]() $P(z)=(\{z\}\times X_{A\backslash \Gamma })\cap P$
for all
$P(z)=(\{z\}\times X_{A\backslash \Gamma })\cap P$
for all
![]() $z\in P_{\Gamma }$
. This implies that each
$z\in P_{\Gamma }$
. This implies that each
![]() $P(z)$
is
$P(z)$
is
![]() $\tau $
-negligible in
$\tau $
-negligible in
![]() $\{z\}\times X_{A\backslash \Gamma }$
. Otherwise,
$\{z\}\times X_{A\backslash \Gamma }$
. Otherwise,
![]() $P(z^*)$
would contain a closed
$P(z^*)$
would contain a closed
![]() $G_{\lambda }$
-set in
$G_{\lambda }$
-set in
![]() $\{z^{*}\}\times X_{A\backslash \Gamma }$
for some
$\{z^{*}\}\times X_{A\backslash \Gamma }$
for some
![]() $z^*\in P_{\Gamma }$
and
$z^*\in P_{\Gamma }$
and
![]() $\lambda <\tau $
. Because
$\lambda <\tau $
. Because
![]() $\{z^*\}\times X_{A\backslash \Gamma }$
is
$\{z^*\}\times X_{A\backslash \Gamma }$
is
![]() $G_{\mu }$
-set in X, where
$G_{\mu }$
-set in X, where
![]() $\mu $
is the cardinality of
$\mu $
is the cardinality of
![]() $\Gamma $
,
$\Gamma $
,
![]() $P(z^*)$
contains a
$P(z^*)$
contains a
![]() $G_{\lambda '}$
-subset of X with
$G_{\lambda '}$
-subset of X with
![]() $\lambda '=\max \{\lambda ,\mu \}<\tau $
, a contradiction.
$\lambda '=\max \{\lambda ,\mu \}<\tau $
, a contradiction.
Using the above observation, we can apply Lemma 2.2 countably many times to construct by induction a disjoint sequence
![]() $\{C_n\}$
of finite subsets of
$\{C_n\}$
of finite subsets of
![]() $A\backslash C$
such that:
$A\backslash C$
such that:
-
•
 $C_1\subset A\backslash C$
.
$C_1\subset A\backslash C$
. -
•
 $C_{n+1}\subset A\backslash \bigcup _{k\leq n}C\cup C_k$
.
$C_{n+1}\subset A\backslash \bigcup _{k\leq n}C\cup C_k$
. -
•
 $P_{C_n}\neq X_{C_n}$
for all n.
$P_{C_n}\neq X_{C_n}$
for all n.
Indeed, suppose that we already constructed the sets
![]() $C_k$
,
$C_k$
,
![]() $k=1,2,\ldots ,n$
. Since the cardinality of
$k=1,2,\ldots ,n$
. Since the cardinality of
![]() $C_n'=\bigcup _{k\leq n}C\cup C_k$
is
$C_n'=\bigcup _{k\leq n}C\cup C_k$
is
![]() $<\tau $
,
$<\tau $
,
![]() $(\{z\}\times X_{A\backslash C_n'})\cap P$
is
$(\{z\}\times X_{A\backslash C_n'})\cap P$
is
![]() $\tau $
-negligible in
$\tau $
-negligible in
![]() $\{z\}\times X_{A\backslash C_n'}$
for every
$\{z\}\times X_{A\backslash C_n'}$
for every
![]() $z\in P_{C_n'}$
. Then, by Lemma 2.2,
$z\in P_{C_n'}$
. Then, by Lemma 2.2,
![]() $P_{A\backslash C_n'}\neq X_{A\backslash C_n'}$
. Hence, we can choose a finite set
$P_{A\backslash C_n'}\neq X_{A\backslash C_n'}$
. Hence, we can choose a finite set
![]() $C_{n+1}\subset A\backslash C_n'$
and an open set
$C_{n+1}\subset A\backslash C_n'$
and an open set
![]() $V\subset X_{C_{n+1}}$
such that
$V\subset X_{C_{n+1}}$
such that
![]() $V\times X_{A\backslash (C_n'\cup C_{n+1})}$
is disjoint from
$V\times X_{A\backslash (C_n'\cup C_{n+1})}$
is disjoint from
![]() $P_{A\backslash C_n'}$
. This implies
$P_{A\backslash C_n'}$
. This implies
![]() $P_{C_{n+1}}\neq X_{C_{n+1}}$
.
$P_{C_{n+1}}\neq X_{C_{n+1}}$
.
One can show that
![]() $B=\bigcup _{n\geq 1}C\cup C_n$
is the required set.
$B=\bigcup _{n\geq 1}C\cup C_n$
is the required set.
If
![]() $f:P\to P$
is a homeomorphism and C is f-admissible, then for every
$f:P\to P$
is a homeomorphism and C is f-admissible, then for every
![]() $\alpha \in A$
, fix a countable f-admissible set
$\alpha \in A$
, fix a countable f-admissible set
![]() $B(\alpha )$
containing
$B(\alpha )$
containing
![]() $\alpha $
(see Proposition 2.1). Next, using Lemma 2.2, we construct a disjoint sequence
$\alpha $
(see Proposition 2.1). Next, using Lemma 2.2, we construct a disjoint sequence
![]() $\{C_n\}$
of finite sets with:
$\{C_n\}$
of finite sets with:
-
•
 $C_1\subset A\backslash C$
;
$C_1\subset A\backslash C$
; -
•
 $C_{n+1}\subset A\backslash \bigcup _{k\leq n}C\cup C_k'$
, where
$C_{n+1}\subset A\backslash \bigcup _{k\leq n}C\cup C_k'$
, where
 $C_k'=\bigcup _{\alpha \in C_k}B(\alpha )$
;
$C_k'=\bigcup _{\alpha \in C_k}B(\alpha )$
; -
•
 $P_{C_n}\neq X_{C_n}$
for all n.
$P_{C_n}\neq X_{C_n}$
for all n.
Then
![]() $B=\bigcup _{n\geq 1}C\cup C_n'$
is f-admissible and satisfies the required conditions.
$B=\bigcup _{n\geq 1}C\cup C_n'$
is f-admissible and satisfies the required conditions.
Everywhere below by
![]() ${\mathcal H}(X)$
we denote the space of all autohomeomorphisms of X with the compact-open topology.
${\mathcal H}(X)$
we denote the space of all autohomeomorphisms of X with the compact-open topology.
Lemma 2.4 Let
![]() $X=\prod _{\alpha \in A}X_{\alpha }$
be a product of zero-dimensional compact metric spaces, and let P be a closed set in X. Suppose that f is an autohomeomorphism of P and that there exist a proper subset
$X=\prod _{\alpha \in A}X_{\alpha }$
be a product of zero-dimensional compact metric spaces, and let P be a closed set in X. Suppose that f is an autohomeomorphism of P and that there exist a proper subset
![]() $B\subset A$
and an autohomeomorphism
$B\subset A$
and an autohomeomorphism
![]() $f_B$
of
$f_B$
of
![]() $P_B$
such that:
$P_B$
such that:
-
•
 $A\backslash B$
is countable and
$A\backslash B$
is countable and
 $P=P_{B}\times X_{A\backslash B}$
.
$P=P_{B}\times X_{A\backslash B}$
. -
•
 $f_B\circ \pi _B=\pi _B\circ f$
.
$f_B\circ \pi _B=\pi _B\circ f$
. -
•
 $f_B$
can be extended to a homeomorphism
$f_B$
can be extended to a homeomorphism
 ${\widetilde f}_B\in {\mathcal H}(X_B)$
.
${\widetilde f}_B\in {\mathcal H}(X_B)$
.
Then f can be extended to a homeomorphism
![]() ${\widetilde f}\in {\mathcal H}(X)$
such that
${\widetilde f}\in {\mathcal H}(X)$
such that
![]() ${\widetilde f}_B\circ \pi _B=\pi _B\circ {\widetilde f}$
.
${\widetilde f}_B\circ \pi _B=\pi _B\circ {\widetilde f}$
.
Proof Since
![]() $f_B\circ \pi _B=\pi _B\circ f$
, f is of the form
$f_B\circ \pi _B=\pi _B\circ f$
, f is of the form
![]() $f(x,y)=(f_B(x),h(x,y))$
with
$f(x,y)=(f_B(x),h(x,y))$
with
![]() $(x,y)\in P_{B}\times X_{A\backslash B}$
such that for each
$(x,y)\in P_{B}\times X_{A\backslash B}$
such that for each
![]() $x\in P_{B}$
, the map
$x\in P_{B}$
, the map
![]() $\varphi _x$
, defined by
$\varphi _x$
, defined by
![]() $\varphi _x(y)=h(x,y)$
, belongs to
$\varphi _x(y)=h(x,y)$
, belongs to
![]() ${\mathcal H}(X_{A\backslash B})$
. So, we have a map
${\mathcal H}(X_{A\backslash B})$
. So, we have a map
![]() $\varphi :P_{B}\to {\mathcal H}(X_{A\backslash B})$
(see [Reference Engelking4, Theorem 3.4.9]). Because
$\varphi :P_{B}\to {\mathcal H}(X_{A\backslash B})$
(see [Reference Engelking4, Theorem 3.4.9]). Because
![]() ${\mathcal H}(X_{A\backslash B})$
is a complete separable metric space, it is an absolute extensor for zero-dimensional compacta (for example, this follows from Michael’s zero-dimensional selection theorem [Reference Michael9]). Hence,
${\mathcal H}(X_{A\backslash B})$
is a complete separable metric space, it is an absolute extensor for zero-dimensional compacta (for example, this follows from Michael’s zero-dimensional selection theorem [Reference Michael9]). Hence,
![]() $\varphi $
can be extended to a map
$\varphi $
can be extended to a map
![]() $\widetilde \varphi : X_B\to {\mathcal H}(X_{A\backslash B})$
. Define
$\widetilde \varphi : X_B\to {\mathcal H}(X_{A\backslash B})$
. Define
![]() $\widetilde h:X\to X_{A\backslash B}$
,
$\widetilde h:X\to X_{A\backslash B}$
,
![]() $\widetilde h(x,y)=\widetilde \varphi (x)(y)$
, where
$\widetilde h(x,y)=\widetilde \varphi (x)(y)$
, where
![]() $(x,y)\in X_B\times X_{A\backslash B}$
. Finally,
$(x,y)\in X_B\times X_{A\backslash B}$
. Finally,
![]() ${\widetilde f}(x,y)=({\widetilde f}_B,\widetilde h(x,y))$
provides a homeomorphism in
${\widetilde f}(x,y)=({\widetilde f}_B,\widetilde h(x,y))$
provides a homeomorphism in
![]() ${\mathcal H}(X)$
extending f such that
${\mathcal H}(X)$
extending f such that
![]() ${\widetilde f}_B\circ \pi _B=\pi _B\circ {\widetilde f}$
.
${\widetilde f}_B\circ \pi _B=\pi _B\circ {\widetilde f}$
.
3 Extending homeomorphisms
In this section, we provide a proof of Theorem 1.2. Everywhere below, we denote by
![]() $\mathfrak {C}$
the Cantor set. Recall that
$\mathfrak {C}$
the Cantor set. Recall that
![]() $\mathfrak {C}$
is the unique zero-dimensional perfect compact metrizable space [Reference Brouwer1].
$\mathfrak {C}$
is the unique zero-dimensional perfect compact metrizable space [Reference Brouwer1].
Lemma 3.1 Let X be a zero-dimensional paracompact space. Suppose that
![]() $P'\subset X\times \mathfrak {C}$
is a closed set such that
$P'\subset X\times \mathfrak {C}$
is a closed set such that
![]() $\pi _X(P')=X$
and that
$\pi _X(P')=X$
and that
![]() $f\in {\mathcal H}(P')$
and
$f\in {\mathcal H}(P')$
and
![]() $g\in {\mathcal H}(X)$
are homeomorphisms with
$g\in {\mathcal H}(X)$
are homeomorphisms with
![]() $g\circ \pi _X=\pi _{X}\circ f$
. If the set
$g\circ \pi _X=\pi _{X}\circ f$
. If the set
![]() $\pi _{\mathfrak {C}}((\{x\}\times \mathfrak {C})\cap P')$
is nowhere dense in
$\pi _{\mathfrak {C}}((\{x\}\times \mathfrak {C})\cap P')$
is nowhere dense in
![]() $\mathfrak {C}$
for all
$\mathfrak {C}$
for all
![]() $x\in X$
, then f can be extended to a homeomorphism
$x\in X$
, then f can be extended to a homeomorphism
![]() ${\widetilde f}\in {\mathcal H}(X\times \mathfrak {C})$
such that
${\widetilde f}\in {\mathcal H}(X\times \mathfrak {C})$
such that
![]() $g\circ \pi _X=\pi _{X}\circ {\widetilde f}$
.
$g\circ \pi _X=\pi _{X}\circ {\widetilde f}$
.
Proof For any
![]() $x\in X$
, let
$x\in X$
, let
![]() $\Phi (x)$
be the set of all
$\Phi (x)$
be the set of all
![]() $h\in {\mathcal H}(\mathfrak {C})$
such that
$h\in {\mathcal H}(\mathfrak {C})$
such that
![]() $f(x,c)=(g(x),h(c))$
for all
$f(x,c)=(g(x),h(c))$
for all
![]() $c\in \pi _X^{-1}(x)\cap P'$
. Since
$c\in \pi _X^{-1}(x)\cap P'$
. Since
![]() $f|(\pi _X^{-1}(x)\cap P')$
is a homeomorphism between the nowhere dense subsets
$f|(\pi _X^{-1}(x)\cap P')$
is a homeomorphism between the nowhere dense subsets
![]() $\pi _{\mathfrak {C}}((\{x\}\times \mathfrak {C})\cap P')$
and
$\pi _{\mathfrak {C}}((\{x\}\times \mathfrak {C})\cap P')$
and
![]() $\pi _{\mathfrak {C}}((\{g(x)\}\times \mathfrak {C})\cap P')$
of
$\pi _{\mathfrak {C}}((\{g(x)\}\times \mathfrak {C})\cap P')$
of
![]() $\mathfrak {C}$
, Knaster–Reichbach’s theorem [Reference Knaster and Reichbach5] cited above yields a homeomorphism
$\mathfrak {C}$
, Knaster–Reichbach’s theorem [Reference Knaster and Reichbach5] cited above yields a homeomorphism
![]() $h_x\in \mathcal {H}(\mathfrak {C})$
extending
$h_x\in \mathcal {H}(\mathfrak {C})$
extending
![]() $f|(\pi _X^{-1}(x)\cap P')$
. Hence,
$f|(\pi _X^{-1}(x)\cap P')$
. Hence,
![]() $\Phi (x)\neq \varnothing $
for all
$\Phi (x)\neq \varnothing $
for all
![]() $x\in X$
. Moreover, the sets
$x\in X$
. Moreover, the sets
![]() $\Phi (x)$
are closed in
$\Phi (x)$
are closed in
![]() ${\mathcal H}(\mathfrak {C})$
equipped with the compact-open topology. So, we have a set-valued map
${\mathcal H}(\mathfrak {C})$
equipped with the compact-open topology. So, we have a set-valued map
![]() $\Phi :X\rightsquigarrow {\mathcal H}(\mathfrak {C})$
. One can show that if
$\Phi :X\rightsquigarrow {\mathcal H}(\mathfrak {C})$
. One can show that if
![]() $\Phi $
admits a continuous selection
$\Phi $
admits a continuous selection
![]() $\phi :X\to {\mathcal H}(\mathfrak {C})$
, then the map
$\phi :X\to {\mathcal H}(\mathfrak {C})$
, then the map
![]() ${\widetilde f}:X\times \mathfrak {C}\to X\times \mathfrak {C}$
, defined by
${\widetilde f}:X\times \mathfrak {C}\to X\times \mathfrak {C}$
, defined by
![]() ${\widetilde f}(x,c)=(g(x),\phi (x)(c))$
, is the required homeomorphism extending f. Therefore, according to Michael’s [Reference Michael9] zero-dimensional selection theorem, it suffices to show that
${\widetilde f}(x,c)=(g(x),\phi (x)(c))$
, is the required homeomorphism extending f. Therefore, according to Michael’s [Reference Michael9] zero-dimensional selection theorem, it suffices to show that
![]() $\Phi $
is lower semi-continuous, i.e., the set
$\Phi $
is lower semi-continuous, i.e., the set
![]() $\{x\in X:\Phi (x)\cap W\neq \varnothing \}$
is open in X for any open
$\{x\in X:\Phi (x)\cap W\neq \varnothing \}$
is open in X for any open
![]() $W\subset {\mathcal H}(\mathfrak {C})$
.
$W\subset {\mathcal H}(\mathfrak {C})$
.
To prove that, let
![]() $x^{*}\in X$
be a fixed point and
$x^{*}\in X$
be a fixed point and
![]() $h^*\in \Phi (x^{*})\cap W$
, where W is open in
$h^*\in \Phi (x^{*})\cap W$
, where W is open in
![]() ${\mathcal H}(\mathfrak {C})$
. We can assume that W is of the form
${\mathcal H}(\mathfrak {C})$
. We can assume that W is of the form
![]() $\{h\in {\mathcal H}(\mathfrak {C}): h(U_i)\subset V_i, i=1,2,\dots ,k\}$
, where
$\{h\in {\mathcal H}(\mathfrak {C}): h(U_i)\subset V_i, i=1,2,\dots ,k\}$
, where
![]() $\{U_i\}_{i=1}^k$
is a clopen disjoint cover of
$\{U_i\}_{i=1}^k$
is a clopen disjoint cover of
![]() $\{x^*\}\times \mathfrak {C}$
and
$\{x^*\}\times \mathfrak {C}$
and
![]() $\{V_i\}_{i=1}^k$
is a disjoint clopen cover of
$\{V_i\}_{i=1}^k$
is a disjoint clopen cover of
![]() $\{g(x^*)\}\times \mathfrak {C}$
. We extend the sets
$\{g(x^*)\}\times \mathfrak {C}$
. We extend the sets
![]() $U_i$
and
$U_i$
and
![]() $V_i$
to clopen sets
$V_i$
to clopen sets
![]() $\widetilde U_i, \widetilde V_i\subset X\times \mathfrak {C}$
such that:
$\widetilde U_i, \widetilde V_i\subset X\times \mathfrak {C}$
such that:
-
(1)
 $\widetilde U_i=O(x^*)\times U_i$
and
$\widetilde U_i=O(x^*)\times U_i$
and
 $\widetilde V_i=g(O(x^*))\times V_i$
, where
$\widetilde V_i=g(O(x^*))\times V_i$
, where
 $O(x^*)$
is a clopen neighborhood of
$O(x^*)$
is a clopen neighborhood of
 $x^*$
in X.
$x^*$
in X. -
(2)
 $O(x^*)$
can be chosen so small that
$O(x^*)$
can be chosen so small that
 $f(\widetilde U_i\cap P')\subset \widetilde V_i\cap P'$
.
$f(\widetilde U_i\cap P')\subset \widetilde V_i\cap P'$
.
We are going to show that for every
![]() $x\in O(x^*)$
, there exists
$x\in O(x^*)$
, there exists
![]() $h_x\in \Phi (x)\cap W$
. We fix such x and observe that all sets
$h_x\in \Phi (x)\cap W$
. We fix such x and observe that all sets
![]() $\widetilde U_i(x)=\widetilde U_i\cap (\{x\}\times \mathfrak {C})$
and
$\widetilde U_i(x)=\widetilde U_i\cap (\{x\}\times \mathfrak {C})$
and
![]() $\widetilde V_i(x)=\widetilde V_i\cap (\{g(x)\}\times \mathfrak {C})$
are compact and perfect. Moreover,
$\widetilde V_i(x)=\widetilde V_i\cap (\{g(x)\}\times \mathfrak {C})$
are compact and perfect. Moreover,
![]() $\widetilde U_i(x)\cap P'$
and
$\widetilde U_i(x)\cap P'$
and
![]() $\widetilde V_i(x)\cap P'$
are nowhere dense sets in
$\widetilde V_i(x)\cap P'$
are nowhere dense sets in
![]() $\widetilde U_i(x)$
and
$\widetilde U_i(x)$
and
![]() $\widetilde V_i(x)$
, respectively, and
$\widetilde V_i(x)$
, respectively, and
![]() $f^x_i=f|(\widetilde U_i(x)\cap P')$
is a homeomorphism between
$f^x_i=f|(\widetilde U_i(x)\cap P')$
is a homeomorphism between
![]() $\widetilde U_i(x)\cap P'$
and
$\widetilde U_i(x)\cap P'$
and
![]() $\widetilde V_i(x)\cap P'$
. Hence, by Knaster–Reichbach’s theorem [Reference Knaster and Reichbach5], for every i, there exists a homeomorphism
$\widetilde V_i(x)\cap P'$
. Hence, by Knaster–Reichbach’s theorem [Reference Knaster and Reichbach5], for every i, there exists a homeomorphism
![]() ${\widetilde f}^x_i:\widetilde U_i(x)\to \widetilde V_i(x)$
extending
${\widetilde f}^x_i:\widetilde U_i(x)\to \widetilde V_i(x)$
extending
![]() $f^x_i$
. Because
$f^x_i$
. Because
![]() $\{\widetilde U_i(x)\}_{i=1}^k$
and
$\{\widetilde U_i(x)\}_{i=1}^k$
and
![]() $\{\widetilde V_i(x)\}_{i=1}^k$
are disjoint clopen covers of
$\{\widetilde V_i(x)\}_{i=1}^k$
are disjoint clopen covers of
![]() $\pi _X^{-1}(x)$
and
$\pi _X^{-1}(x)$
and
![]() $\pi _X^{-1}(g(x))$
, respectively, the homeomorphisms
$\pi _X^{-1}(g(x))$
, respectively, the homeomorphisms
![]() ${\widetilde f}^x_i$
,
${\widetilde f}^x_i$
,
![]() $i=1,2,\ldots ,k$
, provide a homeomorphism
$i=1,2,\ldots ,k$
, provide a homeomorphism
![]() $h_x'$
between
$h_x'$
between
![]() $\pi _X^{-1}(x)$
and
$\pi _X^{-1}(x)$
and
![]() $\pi _X^{-1}(g(x))$
extending
$\pi _X^{-1}(g(x))$
extending
![]() $f|\pi _X^{-1}(x)\cap P'$
. Then the equality
$f|\pi _X^{-1}(x)\cap P'$
. Then the equality
![]() $h_x(c)=h_x'(x,c)$
,
$h_x(c)=h_x'(x,c)$
,
![]() $c\in \mathfrak {C}$
, defines a homeomorphism
$c\in \mathfrak {C}$
, defines a homeomorphism
![]() $h_x\in \mathcal {H}(\mathfrak {C})$
with
$h_x\in \mathcal {H}(\mathfrak {C})$
with
![]() $h_x\in \Phi (x)\cap W$
. Therefore,
$h_x\in \Phi (x)\cap W$
. Therefore,
![]() $\Phi $
is lower semi-continuous.
$\Phi $
is lower semi-continuous.
Proof of Theorem 1.2
We identify
![]() $D^{\tau }$
with
$D^{\tau }$
with
![]() $D^A$
, where A is a set of cardinality
$D^A$
, where A is a set of cardinality
![]() $\tau $
. We already observed that the theorem is true when A is countable. So, let
$\tau $
. We already observed that the theorem is true when A is countable. So, let
![]() $A=\{\alpha :\alpha <\omega (\tau )\}$
be uncountable. Let show that the proof is reduced to the case of one negligible subset
$A=\{\alpha :\alpha <\omega (\tau )\}$
be uncountable. Let show that the proof is reduced to the case of one negligible subset
![]() $P\subset D^A$
and an autohomeomorphism
$P\subset D^A$
and an autohomeomorphism
![]() $f\in {\mathcal H}(P)$
. Indeed, take two disjoint copies X and Y of
$f\in {\mathcal H}(P)$
. Indeed, take two disjoint copies X and Y of
![]() $D^A$
with
$D^A$
with
![]() $P\subset X$
and
$P\subset X$
and
![]() $K\subset Y$
, and let
$K\subset Y$
, and let
![]() $Q=P\biguplus K$
be the disjoint union of P and K. Obviously,
$Q=P\biguplus K$
be the disjoint union of P and K. Obviously,
![]() $X\biguplus Y$
is homeomorphic to
$X\biguplus Y$
is homeomorphic to
![]() $D^A$
, Q is negligible in
$D^A$
, Q is negligible in
![]() $X\biguplus Y$
, and
$X\biguplus Y$
, and
![]() $f\biguplus f^{-1}$
is an autohomeomorphism of Q. Suppose that
$f\biguplus f^{-1}$
is an autohomeomorphism of Q. Suppose that
![]() $f\biguplus f^{-1}$
can be extended to a homeomorphism
$f\biguplus f^{-1}$
can be extended to a homeomorphism
![]() $F:X\biguplus Y\to X\biguplus Y$
. Choose two clopen neighborhoods
$F:X\biguplus Y\to X\biguplus Y$
. Choose two clopen neighborhoods
![]() $X'$
and
$X'$
and
![]() $Y'$
of
$Y'$
of
![]() $P$
and
$P$
and
![]() $K$
in
$K$
in
![]() $X$
and
$X$
and
![]() $Y$
, respectively, with
$Y$
, respectively, with
![]() $X\backslash X'\neq\varnothing\neq Y\backslash Y'$
such that
$X\backslash X'\neq\varnothing\neq Y\backslash Y'$
such that
![]() $F(X')=Y'$
. Then there is a homeomorphism
$F(X')=Y'$
. Then there is a homeomorphism
![]() $G:X\backslash X'\to Y\backslash Y'$
. Hence,
$G:X\backslash X'\to Y\backslash Y'$
. Hence,
![]() $F|X'$
and G provide a homeomorphism
$F|X'$
and G provide a homeomorphism
![]() ${\widetilde f}:X\to Y$
extending f. Therefore, we can suppose that we have one negligible subset P of
${\widetilde f}:X\to Y$
extending f. Therefore, we can suppose that we have one negligible subset P of
![]() $D^A$
and an autohomeomorphism
$D^A$
and an autohomeomorphism
![]() $f\in {\mathcal H}(P)$
.
$f\in {\mathcal H}(P)$
.
We identify
![]() $D^A$
with
$D^A$
with
![]() $X=\mathfrak {C}^A$
and take a functionally open set
$X=\mathfrak {C}^A$
and take a functionally open set
![]() $V(P)$
in X which is dense in
$V(P)$
in X which is dense in
![]() $X\setminus P$
. Because every continuous function on X depends on countably many coordinates, we can choose a countable set
$X\setminus P$
. Because every continuous function on X depends on countably many coordinates, we can choose a countable set
![]() $C\subset A$
such that
$C\subset A$
such that
![]() $\pi _C^{-1}(\pi _C(V(P)))=V(P)$
. Hence,
$\pi _C^{-1}(\pi _C(V(P)))=V(P)$
. Hence,
![]() $P_B$
is a nowhere dense subset of
$P_B$
is a nowhere dense subset of
![]() $X_B$
for any set
$X_B$
for any set
![]() $B\subset A$
containing C. Next, using Proposition 2.3, we can cover A by an increasing transfinite family
$B\subset A$
containing C. Next, using Proposition 2.3, we can cover A by an increasing transfinite family
![]() $\{A(\alpha ):\alpha <\omega (\tau )\}$
and find homeomorphisms
$\{A(\alpha ):\alpha <\omega (\tau )\}$
and find homeomorphisms
![]() $f_{\alpha }\in {\mathcal H}(P_{A(\alpha )})$
satisfying the following conditions:
$f_{\alpha }\in {\mathcal H}(P_{A(\alpha )})$
satisfying the following conditions:
-
(3)
 $A(1)$
is countable and the cardinality of each
$A(1)$
is countable and the cardinality of each
 $A(\alpha )$
is less than
$A(\alpha )$
is less than
 $\tau $
.
$\tau $
. -
(4)
 $A_{\alpha }=\bigcup _{\beta <\alpha }A(\beta )$
if
$A_{\alpha }=\bigcup _{\beta <\alpha }A(\beta )$
if
 $\alpha $
is a limit ordinal.
$\alpha $
is a limit ordinal. -
(5)
 $A(\alpha +1)\backslash A(\alpha )$
is countable and
$A(\alpha +1)\backslash A(\alpha )$
is countable and
 $C\subset A(\alpha )$
for all
$C\subset A(\alpha )$
for all
 $\alpha $
.
$\alpha $
. -
(6)
 $\displaystyle \pi _{A(\alpha )}\circ f=f_{\alpha }\circ \pi _{A(\alpha )}$
.
$\displaystyle \pi _{A(\alpha )}\circ f=f_{\alpha }\circ \pi _{A(\alpha )}$
. -
(7) Each
 $P_{A(\alpha +1)\backslash A(\alpha )}$
is a nowhere dense set in
$P_{A(\alpha +1)\backslash A(\alpha )}$
is a nowhere dense set in
 $X_{A(\alpha +1)\backslash A(\alpha )}$
.
$X_{A(\alpha +1)\backslash A(\alpha )}$
.
It remains to prove that each
![]() $f_{\alpha }$
can be extended to a homeomorphism
$f_{\alpha }$
can be extended to a homeomorphism
![]() ${\widetilde f}_{\alpha }\in {\mathcal H}(X_{A(\alpha )})$
such that
${\widetilde f}_{\alpha }\in {\mathcal H}(X_{A(\alpha )})$
such that
-
(8)
 $\displaystyle \pi _{A(\alpha )}^{A(\alpha +1)}\circ {\widetilde f}_{\alpha +1}=\widetilde f_{\alpha }\circ \pi _{A(\alpha )}^{A(\alpha +1)}$
.
$\displaystyle \pi _{A(\alpha )}^{A(\alpha +1)}\circ {\widetilde f}_{\alpha +1}=\widetilde f_{\alpha }\circ \pi _{A(\alpha )}^{A(\alpha +1)}$
.
The proof is by transfinite induction. The first extension
![]() ${\widetilde f}_1$
exists by Knaster–Reichbach’s theorem [Reference Knaster and Reichbach5] because
${\widetilde f}_1$
exists by Knaster–Reichbach’s theorem [Reference Knaster and Reichbach5] because
![]() $P_{A(1)}$
is nowhere dense in
$P_{A(1)}$
is nowhere dense in
![]() $X_{A(1)}$
. If
$X_{A(1)}$
. If
![]() ${\widetilde f}_{\alpha }$
is already defined for all
${\widetilde f}_{\alpha }$
is already defined for all
![]() $\alpha <\beta $
, where
$\alpha <\beta $
, where
![]() $\beta $
is a limit ordinal, then item (4) implies the existence of
$\beta $
is a limit ordinal, then item (4) implies the existence of
![]() ${\widetilde f}_{\beta }$
. Therefore, we need only to define
${\widetilde f}_{\beta }$
. Therefore, we need only to define
![]() ${\widetilde f}_{\alpha +1}$
provided
${\widetilde f}_{\alpha +1}$
provided
![]() ${\widetilde f}_{\alpha }$
exists.
${\widetilde f}_{\alpha }$
exists.
To this end, consider the space
![]() $P_{A(\alpha )}\times X_{A(\alpha +1)\backslash A(\alpha )}$
, the set
$P_{A(\alpha )}\times X_{A(\alpha +1)\backslash A(\alpha )}$
, the set
![]() $P'=P_{A(\alpha +1)}\subset P_{A(\alpha )}\times X_{A(\alpha +1)\backslash A(\alpha )}$
, and the homeomorphisms
$P'=P_{A(\alpha +1)}\subset P_{A(\alpha )}\times X_{A(\alpha +1)\backslash A(\alpha )}$
, and the homeomorphisms
![]() $f_{\alpha +1}$
,
$f_{\alpha +1}$
,
![]() $f_{\alpha }$
. For any
$f_{\alpha }$
. For any
![]() $x\in P_{A(\alpha )}$
, consider the set
$x\in P_{A(\alpha )}$
, consider the set
Item (7) yields that
![]() $\pi _{A(\alpha +1)\backslash A(\alpha )}(P'(x))$
is nowhere dense in
$\pi _{A(\alpha +1)\backslash A(\alpha )}(P'(x))$
is nowhere dense in
![]() $X_{A(\alpha +1)\backslash A(\alpha )}$
for every
$X_{A(\alpha +1)\backslash A(\alpha )}$
for every
![]() $x\in P_{A(\alpha )}$
. Therefore, by Lemma 3.1, the homeomorphism
$x\in P_{A(\alpha )}$
. Therefore, by Lemma 3.1, the homeomorphism
![]() $f_{\alpha +1}$
can be extended to a homeomorphism
$f_{\alpha +1}$
can be extended to a homeomorphism
such that
![]() $\pi _{A(\alpha )}\circ f_{\alpha +1}'=f_{\alpha }\circ \pi _{A(\alpha )}$
. Finally, by Lemma 2.4, there is a homeomorphism
$\pi _{A(\alpha )}\circ f_{\alpha +1}'=f_{\alpha }\circ \pi _{A(\alpha )}$
. Finally, by Lemma 2.4, there is a homeomorphism
![]() ${\widetilde f}_{\alpha +1}\in {\mathcal H}(\mathfrak {C}^{A(\alpha +1)})$
satisfying condition (8).
${\widetilde f}_{\alpha +1}\in {\mathcal H}(\mathfrak {C}^{A(\alpha +1)})$
satisfying condition (8).
Acknowledgment
The authors would like to express their gratitude to J. van Mill for his observation that the condition
![]() $\tau>\aleph _0$
in Lemma 2.2 is essential. We also thank the referee for his/her careful reading and helpful comments.
$\tau>\aleph _0$
in Lemma 2.2 is essential. We also thank the referee for his/her careful reading and helpful comments.