Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lambek, J.
1971.
On the Representation of Modules by Sheaves of Factor Modules.
Canadian Mathematical Bulletin,
Vol. 14,
Issue. 3,
p.
359.
Hofmann, Karl Heinrich
1972.
Representations of algebras by continuous sections.
Bulletin of the American Mathematical Society,
Vol. 78,
Issue. 3,
p.
291.
Shin, Gooyong
1973.
Prime ideals and sheaf representation of a pseudo symmetric ring.
Transactions of the American Mathematical Society,
Vol. 184,
Issue. 0,
p.
43.
Davis, G.
1973.
Representation and extension of semiprime rings.
Journal of the Australian Mathematical Society,
Vol. 15,
Issue. 3,
p.
353.
Lanski, Charles
1974.
Rings with involution which are I-rings.
Journal of Algebra,
Vol. 32,
Issue. 1,
p.
109.
Szeto, George
1975.
On almost hereditary rings.
Journal of Algebra,
Vol. 34,
Issue. 1,
p.
97.
Cornish, William H.
1975.
Boolean orthogonalities and minimal prime ideals.
Communications in Algebra,
Vol. 3,
Issue. 10,
p.
859.
Stewart, P. N.
1976.
Radicals and functional representations.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 27,
Issue. 3-4,
p.
319.
Szeto, George
1977.
On Sheaf Representation of a Biregular Near-Ring.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 4,
p.
495.
Szeto, George
1977.
On a sheaf representation of a class of near-rings.
Journal of the Australian Mathematical Society,
Vol. 23,
Issue. 1,
p.
78.
Szeto, George
1977.
The sheaf representation of near-rings and its applications.
Communications in Algebra,
Vol. 5,
Issue. 7,
p.
773.
Rai, R. K.
1980.
Orthogonal Completions of Reduced Rings with Respect to Abian Order.
Canadian Mathematical Bulletin,
Vol. 23,
Issue. 4,
p.
477.
Andrunakievich, V. A.
Arnautov, V. I.
Goyan, I. M.
and
Ryabukhin, Yu. M.
1980.
Associative rings.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 1,
p.
922.
Thakare, N.K.
and
Nimbhorkar, S.K.
1983.
Space of minimal prime ideals of a ring without nilpotent elements.
Journal of Pure and Applied Algebra,
Vol. 27,
Issue. 1,
p.
75.
Marconi, Umberto
1984.
On the bear rings.
Journal of Pure and Applied Algebra,
Vol. 33,
Issue. 2,
p.
159.
Simmons, Harold
1985.
Sheaf representations of strongly harmonic rings.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 99,
Issue. 3-4,
p.
249.
Henriksen, M.
and
Kopperman, R.
1991.
A general theory of structure spaces with applications to spaces of prime ideals.
Algebra Universalis,
Vol. 28,
Issue. 3,
p.
349.
Sun, Shu-Hao
1991.
Noncommutative rings in which every prime ideal is contained in a unique maximal ideal.
Journal of Pure and Applied Algebra,
Vol. 76,
Issue. 2,
p.
179.
Sun, Shu-Hao
1992.
A remark on Gelfand duality.
Bulletin of the Australian Mathematical Society,
Vol. 46,
Issue. 2,
p.
187.
Henriksen, Melvin
and
Larson, Suzanne
1993.
Ordered Algebraic Structures.
p.
159.

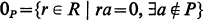 . In this note we will show, this type of representation of a noncommutative ring is possible if the ring contains no nonzero nilpotent elements.
. In this note we will show, this type of representation of a noncommutative ring is possible if the ring contains no nonzero nilpotent elements.