Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-24T18:39:49.409Z Has data issue: false hasContentIssue false
  • English
  • Français

On Delay Differential Inequalities of Higher Order

Published online by Cambridge University Press:  20 November 2018

G. Ladas  and
I. P. Stavroulakis
G. Ladas
Affiliation:
Department of Mathematics, University of Rhode Island, Kingston, RI 02881, U.S.A
I. P. Stavroulakis
Affiliation:
Department of Mathematics, University of Ioannina, Ioannina, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

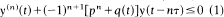Consider the nth order (n ≥ 1) delay differential inequalities and 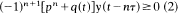and the delay differential equation 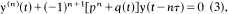, where q(t) ≥ 0 is a continuous function and p, τ are positive constants. Under the condition pτe ≥ 1 we prove that when n is odd (1) has no eventually positive solutions, (2) has no eventually negative solutions, and (3) has only oscillatory solutions and when n is even (1) has no eventually negative bounded solutions, (2) has no eventually positive bounded solutions, and every bounded solution of (3) is oscillatory. The condition pτe > 1 is sharp. The above results, which generalize previous results by Ladas and by Ladas and Stavroulakis for first order delay differential inequalities, are caused by the retarded argument and do not hold when τ = 0.

Keywords

34K1534C10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 25 , Issue 3 , 01 September 1982 , pp. 348 - 354
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Kusano, T. and Onose, H., Oscillations of Functional Differential Equations with Retarded Argument, J. Differentia. Equation. 15 (1974), 269-277.Google Scholar
2. Ladas, G., Lakshmikantham, V. and Papadakis, J. S., Oscillations of higher-order retarded differential equations generated by the retarded argument, Delay and Functional Differential Equations and their Applications, Academic Press, New York, 1972, 219-231.Google Scholar
3. Ladas, G., Sharp Conditions for Oscillations Caused by Delays, Applicable Analysis 9 (1979), 93-98.Google Scholar
4. G. Ladas and Stavroulakis, I. P., On delay differential inequalities of first order, Abstracts Amer. Math. Soc. 1 (1980) no. 6 p. 577. to appear in Funkcial. Ekvac.Google Scholar
5. Naito, M., Oscillations of differential inequalities with retarded arguments, Hiroshima Math, J. 5 (1975), 187-192.Google Scholar
6. Sficas, Y. G., Strongly Monotone Solutions of Retarded Differential Equations, Canad. Math. Bull. 22(4) (1979), 403-412.Google Scholar
7. Staikos, V. A. and Stavroulakis, I. P., Bounded oscillations under the effect of retardations for differential equations of arbitrary order, Proc. Roy. Soc. Edinburgh 77A (1977), 129-136.Google Scholar