Article contents
On Certain Multivariable Subnormal Weighted Shifts and their Duals
Published online by Cambridge University Press: 20 November 2018
Abstract
For every subnormal  $m$ -variable weighted shift
$m$ -variable weighted shift  $S$ (with bounded positive weights), there is a corresponding positive Reinhardt measure
$S$ (with bounded positive weights), there is a corresponding positive Reinhardt measure  $\mu $ supported on a compact Reinhardt subset of
$\mu $ supported on a compact Reinhardt subset of  ${{\mathbb{C}}^{m}}$ . We show that, for
${{\mathbb{C}}^{m}}$ . We show that, for 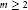 $m\,\ge \,2$ , the dimensions of the 1-st cohomology vector spaces associated with the Koszul complexes of
$m\,\ge \,2$ , the dimensions of the 1-st cohomology vector spaces associated with the Koszul complexes of  $S$ and its dual
$S$ and its dual 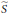 $\widetilde{S}$ are different if a certain radial function happens to be integrable with respect to μ (which is indeed the case with many classical examples). In particular,
$\widetilde{S}$ are different if a certain radial function happens to be integrable with respect to μ (which is indeed the case with many classical examples). In particular,  $S$ cannot in that case be similar to
$S$ cannot in that case be similar to 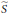 $\widetilde{S}$ . We next prove that, for
$\widetilde{S}$ . We next prove that, for 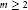 $m\,\ge \,2$ , a Fredholm subnormal
$m\,\ge \,2$ , a Fredholm subnormal  $m$ -variable weighted shift
$m$ -variable weighted shift  $S$ cannot be similar to its dual.
$S$ cannot be similar to its dual.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 2
- Cited by

