Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-11T15:41:19.307Z Has data issue: false hasContentIssue false
  • English
  • Français

On a conjecture of M. R. Murty and V. K. Murty

Part of: Multiplicative number theory

Published online by Cambridge University Press:  25 October 2022

Yuchen Ding Open the ORCID record for Yuchen Ding [Opens in a new window]
Yuchen Ding*
Affiliation:
School of Mathematical Science, Yangzhou University, Yangzhou 225002, P.R. China
*
e-mail: ycding@yzu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 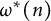$\omega ^*(n)$ be the number of primes p such that 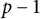$p-1$ divides n. Recently, M. R. Murty and V. K. Murty proved that

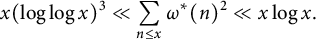$$ \begin{align*}x(\log\log x)^3\ll\sum_{n\le x}\omega^*(n)^2\ll x\log x.\end{align*} $$

They further conjectured that there is some positive constant C such that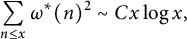

$$ \begin{align*}\sum_{n\le x}\omega^*(n)^2\sim Cx\log x,\end{align*} $$

as 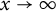$x\rightarrow \infty $ . In this short note, we give the correct order of the sum by showing that

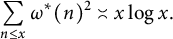$$ \begin{align*}\sum_{n\le x}\omega^*(n)^2\asymp x\log x.\end{align*} $$

Keywords

PrimesBombieri–Vinogradov theoremDichotomy

MSC classification

Primary: 11N25: Distribution of integers with specified multiplicative constraints
Secondary: 11N05: Distribution of primes
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 2 , June 2023 , pp. 679 - 681
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by the National Natural Science Foundation of China under Grant No. 12201544, the Natural Science Foundation of Jiangsu Province of China under Grant No. BK20210784, and the China Postdoctoral Science Foundation under Grant No. 2022M710121. He is also supported by the foundation numbers JSSCBS20211023 and YZLYJF2020PHD051.

References

Davenport, H., Multiplicative number theory. 2nd ed., Graduate Texts in Mathematics, 74, Springer, New York, 1980.CrossRefGoogle Scholar
Erdős, P. and Prachar, K., Über die Anzahl der Lösungen von $\left[p-1,q-1\right]\le x$ . Monatsh. Math. 59(1955), 318–319.CrossRefGoogle Scholar
Hardy, G. H. and Ramanujan, S., The normal number of prime factors of a number $n$ . Quart. J. Math. 48(1917), 76–92.Google Scholar
Murty, M. R. and Murty, V. K., A variant of the Hardy–Ramanujan theorem . Hardy–Ramanujan J. 44(2021), 32–40.Google Scholar
Prachar, K., Über die Anzahl der Teiler einer natürlichen Zahl, welche die Form $p-1$ haben . Monatsh. Math. 59(1955), 91–97.CrossRefGoogle Scholar
Turán, P., On a theorem of Hardy and Ramanujan . J. Lond. Math. Soc. 9(1934), 274–276.CrossRefGoogle Scholar