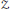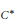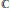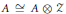Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rørdam, M.
2002.
Classification of Nuclear C*-Algebras. Entropy in Operator Algebras.
Vol. 126,
Issue. ,
p.
1.
RØRDAM, MIKAEL
2004.
THE STABLE AND THE REAL RANK OF ${\mathcal Z}$-ABSORBING C*-ALGEBRAS.
International Journal of Mathematics,
Vol. 15,
Issue. 10,
p.
1065.
Kerr, David
and
Li, Hanfeng
2005.
Dynamical entropy in Banach spaces.
Inventiones mathematicae,
Vol. 162,
Issue. 3,
p.
649.
Toms, Andrew S.
2006.
Flat dimension growth forC∗-algebras.
Journal of Functional Analysis,
Vol. 238,
Issue. 2,
p.
678.
Hirshberg, Ilan
and
Winter, Wilhelm
2007.
Rokhlin actions and self-absorbing C∗-algebras.
Pacific Journal of Mathematics,
Vol. 233,
Issue. 1,
p.
125.
Toms, Andrew S.
2007.
Dimension growth forC∗-algebras.
Advances in Mathematics,
Vol. 213,
Issue. 2,
p.
820.
Hirshberg, Ilan
Rørdam, Mikael
and
Winter, Wilhelm
2007.
$${\mathcal{C}}_{0}$$ (X)-algebras, stability and strongly self-absorbing $${\mathcal{C}}^{*}$$ -algebras.
Mathematische Annalen,
Vol. 339,
Issue. 3,
p.
695.
Perera, Francesc
and
Toms, Andrew S.
2007.
Recasting the Elliott conjecture.
Mathematische Annalen,
Vol. 338,
Issue. 3,
p.
669.
Winter, Wilhelm
2007.
Simple C∗-algebras with locally finite decomposition rank.
Journal of Functional Analysis,
Vol. 243,
Issue. 2,
p.
394.
Toms, Andrew S.
and
Winter, Wilhelm
2008.
-Stable ASH Algebras.
Canadian Journal of Mathematics,
Vol. 60,
Issue. 3,
p.
703.
Elliott, George
and
Toms, Andrew
2008.
Regularity properties in the classification program for separable amenable C*-algebras.
Bulletin of the American Mathematical Society,
Vol. 45,
Issue. 2,
p.
229.
Giol, Julien
and
Kerr, David
2010.
Subshifts and perforation.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 639,
Sato, Yasuhiko
2010.
The Rohlin property for automorphisms of the Jiang–Su algebra.
Journal of Functional Analysis,
Vol. 259,
Issue. 2,
p.
453.
Rørdam, Mikael
and
Winter, Wilhelm
2010.
The Jiang–Su algebra revisited.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 642,
Toms, Andrew
2011.
K-theoretic rigidity and slow dimension growth.
Inventiones mathematicae,
Vol. 183,
Issue. 2,
p.
225.
TIKUISIS, AARON
2011.
THE CUNTZ SEMIGROUP OF CONTINUOUS FUNCTIONS INTO CERTAIN SIMPLE C*-ALGEBRAS.
International Journal of Mathematics,
Vol. 22,
Issue. 08,
p.
1051.
Lin, Huaxin
and
Niu, Zhuang
2011.
The range of a class of classifiable separable simple amenableC∗-algebras.
Journal of Functional Analysis,
Vol. 260,
Issue. 1,
p.
1.
Matui, Hiroki
2011.
Classification of homomorphisms into simpleZ-stableC⁎-algebras.
Journal of Functional Analysis,
Vol. 260,
Issue. 3,
p.
797.
Antoine, Ramon
Dadarlat, Marius
Perera, Francesc
and
Santiago, Luis
2014.
Recovering the Elliott invariant from the Cuntz semigroup.
Transactions of the American Mathematical Society,
Vol. 366,
Issue. 6,
p.
2907.
Brown, Jonathan
and
Hirshberg, Ilan
2014.
The Rokhlin property for endomorphisms and strongly self-absorbing $C^{*}$-algebras.
Illinois Journal of Mathematics,
Vol. 58,
Issue. 3,