No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
We consider the diophantine equation 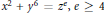 ${{x}^{2}}\,+\,{{y}^{6}}\,=\,{{z}^{e}},\,e\,\le \,4$. We show that, when
${{x}^{2}}\,+\,{{y}^{6}}\,=\,{{z}^{e}},\,e\,\le \,4$. We show that, when  $e$ is a multiple of 4 or 6, this equation has no solutions in positive integers with
$e$ is a multiple of 4 or 6, this equation has no solutions in positive integers with 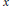 $x$ and
$x$ and  $y$ relatively prime. As a corollary, we show that there exists no primitive Pythagorean triangle one of whose leglengths is a perfect cube, while the hypotenuse length is an integer square.
$y$ relatively prime. As a corollary, we show that there exists no primitive Pythagorean triangle one of whose leglengths is a perfect cube, while the hypotenuse length is an integer square.