Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shashkin, Yu. A.
1975.
Convex sets, extreme points, and simplexes.
Journal of Soviet Mathematics,
Vol. 4,
Issue. 6,
p.
625.

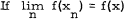 for each extreme point f of the unit ball of N
for each extreme point f of the unit ball of N