Article contents
A Note on Planarity Stratification of Hurwitz Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
One can easily show that any meromorphic function on a complex closed Riemann surface can be represented as a composition of a birational map of this surface to 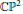 $\mathbb{C}{{\mathbb{P}}^{2}}$ and a projection of the image curve froman appropriate point
$\mathbb{C}{{\mathbb{P}}^{2}}$ and a projection of the image curve froman appropriate point 
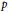 $p$ . We introduce a natural stratification of Hurwitz spaces according to the minimal degree of a plane curve such that a given meromorphic function can be represented in the above way and calculate the dimensions of these strata. We observe that they are closely related to a family of Severi varieties studied earlier by J. Harris, Z. Ran, and I. Tyomkin.
$p$ . We introduce a natural stratification of Hurwitz spaces according to the minimal degree of a plane curve such that a given meromorphic function can be represented in the above way and calculate the dimensions of these strata. We observe that they are closely related to a family of Severi varieties studied earlier by J. Harris, Z. Ran, and I. Tyomkin.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 4
- Cited by

