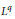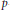Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chang, Liang-Chu
Guo, Cheng-Lin
and
Sung, Chiung-Jue Anna
2010.
p-harmonic 1-forms on complete manifolds.
Archiv der Mathematik,
Vol. 94,
Issue. 2,
p.
183.
Chang, Liang-Chu
and
Sung, Chiung-Jue
2011.
A note onp-harmonicl-forms on complete manifolds.
Pacific Journal of Mathematics,
Vol. 254,
Issue. 2,
p.
295.
Han, Yingbo
and
Pan, Hong
2016.
Lp p-harmonic 1-forms on submanifolds in a Hadamard manifold.
Journal of Geometry and Physics,
Vol. 107,
Issue. ,
p.
79.
Dung, Nguyen Thac
2017.
p-harmonic ℓ-forms on Riemannian manifolds with a weighted Poincaré inequality.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 150,
Issue. ,
p.
138.
Han, Yingbo
2018.
p-Harmonic l-forms on Complete Noncompact Submanifolds in Sphere with Flat Normal Bundle.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 49,
Issue. 1,
p.
107.
Han, Yingbo
2018.
Vanishing Theorem for p-Harmonic 1-Forms on Complete Submanifolds in Spheres.
Bulletin of the Iranian Mathematical Society,
Vol. 44,
Issue. 3,
p.
659.
Dung, Nguyen Thac
and
Sung, Chiung-Jue Anna
2019.
Analysis of weighted p-harmonic forms and applications.
International Journal of Mathematics,
Vol. 30,
Issue. 11,
p.
1950058.
Lin, HeZi
and
Yang, BiaoGui
2020.
The p-eigenvalue estimates and L p-harmonic forms on submanifolds of Hadamard manifolds.
Journal of Mathematical Analysis and Applications,
Vol. 488,
Issue. 1,
p.
124018.
Dong, Yuxin
and
Lin, Hezi
2021.
Gradient Estimate and Liouville Theorems for p-Harmonic Maps.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 8,
p.
8318.
Chao, Xiaoli
Hui, Aiying
and
Bai, Miaomiao
2021.
Vanishing theorems for p-harmonic ℓ-forms on Riemannian manifolds with a weighted Poincaré inequality.
Differential Geometry and its Applications,
Vol. 76,
Issue. ,
p.
101741.
Tuyen, Nguyen Dang
2022.
Vanishing theorems for p-harmonic forms on Riemannian manifolds.
Differential Geometry and its Applications,
Vol. 82,
Issue. ,
p.
101868.
Pham, Duc Thoan
Tran, Van Khien
and
Nguyen, Thi Hong
2023.
On Vanishing Theorems for Locally Conformally Flat Riemannian Manifolds with an Integral Pinching Condition.
Communications in Mathematics and Statistics,
Dung, Ha Tuan
Dung, Nguyen Thac
and
Tuyen, Nguyen Dang
2023.
A Note on p-Harmonic $$\ell $$-Forms on Complete Non-compact Manifolds.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 2,
Pham, Duc Thoan
Nguyen, Dang Tuyen
and
Tran, Van Khien
2023.
Vanishing theorems for complete Riemannian manifolds with weighted p-Poincaré inequality.
Asian-European Journal of Mathematics,
Vol. 16,
Issue. 06,
Jung, Seoung Dal
Qian, Jinhua
and
Fu, Xueshan
2024.
Weighted p-basic harmonic forms and its applications.
Journal of Geometry and Physics,
Vol. 203,
Issue. ,
p.
105241.
Dung, Ha Tuan
Dung, Nguyen Thac
and
Hung, Thieu Dinh Minh
2025.
On vanishing results for smooth metric measure spaces with weighted curvature tensors.
Revista Matemática Complutense,
Nguyen, Dang Tuyen
and
Pyo, Juncheol
2025.
Weighted p-harmonic 1-forms on f-minimal hypersurfaces in smooth metric measure spaces.
International Journal of Mathematics,
Vol. 36,
Issue. 13,
Li, Nan
and
Shen, Zhenghan
2025.
Some vanishing theorems for p-harmonic l-forms on complete Riemannian manifolds.
Differential Geometry and its Applications,
Vol. 100,
Issue. ,
p.
102267.
Dung, Nguyen Thac
Pyo, Juncheol
and
Tuyen, Nguyen Dang
2025.
Vanishing results on weighted manifolds with lower bounds of the curvature operator.
Nonlinear Analysis,
Vol. 260,
Issue. ,
p.
113847.