No CrossRef data available.
Article contents
Non-splitting in Kirchberg's Ideal-related KK-Theory
Published online by Cambridge University Press: 20 November 2018
Abstract
A. Bonkat obtained a universal coefficient theorem in the setting of Kirchberg's ideal-related 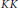 $KK$ -theory in the fundamental case of a
$KK$ -theory in the fundamental case of a 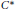 ${{C}^{*}}$ -algebra with one specified ideal. The universal coefficient sequence was shown to split, unnaturally, under certain conditions. Employing certain
${{C}^{*}}$ -algebra with one specified ideal. The universal coefficient sequence was shown to split, unnaturally, under certain conditions. Employing certain  $K$ -theoretical information derivable from the given operator algebras using a method introduced here, we shall demonstrate that Bonkat's
$K$ -theoretical information derivable from the given operator algebras using a method introduced here, we shall demonstrate that Bonkat's 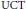 $\text{UCT}$ does not split in general. Related methods lead to information on the complexity of the
$\text{UCT}$ does not split in general. Related methods lead to information on the complexity of the  $K$ -theory which must be used to classify
$K$ -theory which must be used to classify  $*$ -isomorphisms for purely infinite
$*$ -isomorphisms for purely infinite 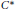 ${{C}^{*}}$ -algebras with one non-trivial ideal.
${{C}^{*}}$ -algebras with one non-trivial ideal.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011

