Article contents
A New Cohomological Criterion for the p-Nilpotence of Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 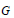 $G$ be a finite group,
$G$ be a finite group, 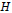 $H$ a copy of its
$H$ a copy of its 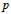 $p$-Sylow subgroup, and
$p$-Sylow subgroup, and 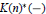 $K{{\left( n \right)}^{*}}\left( - \right)$ the
$K{{\left( n \right)}^{*}}\left( - \right)$ the 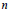 $n$-th Morava
$n$-th Morava 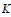 $K$-theory at
$K$-theory at 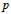 $p$. In this paper we prove that the existence of an isomorphism between
$p$. In this paper we prove that the existence of an isomorphism between 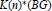 $K{{(n)}^{*}}(BG)$ and
$K{{(n)}^{*}}(BG)$ and 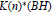 $K{{(n)}^{*}}(BH)$ is a sufficient condition for
$K{{(n)}^{*}}(BH)$ is a sufficient condition for 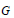 $G$ to be
$G$ to be 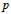 $p$-nilpotent.
$p$-nilpotent.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 3
- Cited by


