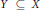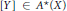Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
King, Ronald C.
Welsh, Trevor A.
and
van Willigenburg, Stephanie J.
2008.
Schur positivity of skew Schur function differences and applications to ribbons and Schubert classes.
Journal of Algebraic Combinatorics,
Vol. 28,
Issue. 1,
p.
139.
Gutschwager, Christian
2010.
On Multiplicity-Free Skew Characters and the Schubert Calculus.
Annals of Combinatorics,
Vol. 14,
Issue. 3,
p.
339.
Bessenrodt, C.
and
van Willigenburg, S.
2013.
Multiplicity Free Schur, Skew Schur, and Quasisymmetric Schur Functions.
Annals of Combinatorics,
Vol. 17,
Issue. 2,
p.
275.
Billey, Sara
and
Pawlowski, Brendan
2014.
Permutation patterns, Stanley symmetric functions, and generalized Specht modules.
Journal of Combinatorial Theory, Series A,
Vol. 127,
Issue. ,
p.
85.
Bessenrodt, Christine
and
Bowman, Christopher
2017.
Multiplicity-free Kronecker products of characters of the symmetric groups.
Advances in Mathematics,
Vol. 322,
Issue. ,
p.
473.
Hodges, Reuven
and
Lakshmibai, Venkatramani
2022.
A classification of spherical Schubert varieties in the Grassmannian.
Proceedings - Mathematical Sciences,
Vol. 132,
Issue. 2,
Gao, Shiliang
Hodges, Reuven
and
Orelowitz, Gidon
2022.
Multiplicity-free skew Schur polynomials.
Algebraic Combinatorics,
Vol. 4,
Issue. 6,
p.
1073.
Zhao, Chenchen
2024.
On the Kronecker product of Schur functions of square shapes.
Algebraic Combinatorics,
Vol. 7,
Issue. 5,
p.
1575.