No CrossRef data available.
Article contents
Multiplicities in the Tensor Product of Finite-Dimensional Representations of Discrete Groups
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let G be a group and ρ and σ two irreducible unitary representations of G in complex Hilbert spaces and assume that dimp ρ= n < ∞. D. Poguntke [2] proved that 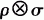 is a sum of at most n2 irreducible subrepresentations. The case when dim a is also finite he attributed to R. Howe.
is a sum of at most n2 irreducible subrepresentations. The case when dim a is also finite he attributed to R. Howe.
We shall prove analogous results for arbitrary finite-dimensional representations, not necessarily unitary. Thus let F be an algebraically closed field of characteristic 0. We shall use the language of modules and we postulate that allour modules are finite-dimensional as F-vector spaces. The field F itself will be considered as a trivial G-module.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1978
References
1.
Hochschild, G.: Introduction to affine algebraic groups, Holden-Day, San Francisco 1971.Google Scholar
2.
Poguntke, D.: Decomposition of tensor products of irreducible unitary representations, Proc. Amer. Math-Soc. 52 (1975), 427-432.Google Scholar

