No CrossRef data available.
Article contents
Maximal Sublattices of Finite Distributive Lattices. III: A Conjecture from the 1984 Banff Conference on Graphs and Order
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let  $L$ be a finite distributive lattice. Let
$L$ be a finite distributive lattice. Let 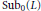 $\text{Su}{{\text{b}}_{0}}(L)$ be the lattice
$\text{Su}{{\text{b}}_{0}}(L)$ be the lattice
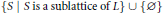 $$\{S\,|\,S\,\text{is}\,\text{a sublattice of }L\}\cup \{\phi \}$$
$$\{S\,|\,S\,\text{is}\,\text{a sublattice of }L\}\cup \{\phi \}$$
and let 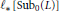 ${{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(L)]$ be the length of the shortest maximal chain in
${{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(L)]$ be the length of the shortest maximal chain in 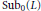 $\text{Su}{{\text{b}}_{0}}(L)$ . It is proved that if
$\text{Su}{{\text{b}}_{0}}(L)$ . It is proved that if 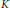 $K$ and
$K$ and  $L$ are non-trivial finite distributive lattices, then
$L$ are non-trivial finite distributive lattices, then
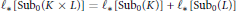 $${{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(K\times L)]={{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(K)]+{{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(L)]$$
$${{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(K\times L)]={{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(K)]+{{\ell }_{*}}[\text{Su}{{\text{b}}_{0}}(L)]$$
A conjecture from the 1984 Banff Conference on Graphs and Order is thus proved.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
[1] Adams, M. E., Dwinger, P., and Schmid, J., Maximal sublattices of finite distributive lattices. Algebra Universalis
36(1996), no. 4, 488–504.Google Scholar
[2] Birkhoff, G., Lattice Theory.
Third edition. American Mathematical Society Colloquium Publications 25, American Mathematical Society, Providence, RI, 1967.Google Scholar
[3] Chen, C. C., Koh, K. M., and Lee, S. C., On the grading numbers of direct products of chains. Discrete Math.
49(1984), no. 1, 21–26.Google Scholar
[4] Davey, B. A. and Priestley, H. A., Introduction to Lattices and Order.
Second edition. Cambridge University Press, Cambridge, 2002.Google Scholar
[6] Rival, I., Maximal sublattices of finite distributive lattices. Proc. Amer. Math. Soc.
37(1973), 417–420.Google Scholar
[7] Rival, I., Maximal sublattices of finite distributive lattices. II. Proc. Amer. Math. Soc.
44(1974), 263–268.Google Scholar

