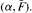Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bonilla, A.
and
Fariña, J.
2001.
𝐿𝑖𝑝𝛼 harmonic approximation on closed sets.
Proceedings of the American Mathematical Society,
Vol. 129,
Issue. 9,
p.
2741.