Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beidar, K.I
Brešar, M
Chebotar, M.A
and
Martindale, W.S
2001.
On Herstein's Lie Map Conjectures, II.
Journal of Algebra,
Vol. 238,
Issue. 1,
p.
239.
Beidar, K. I.
and
Chebotar, M. A.
2001.
ON SURJECTIVE LIE HOMOMORPHISMS ONTO LIE IDEALS OF PRIME RINGS.
Communications in Algebra,
Vol. 29,
Issue. 10,
p.
4775.
Beidar, K. I.
and
Chebotar, M. A.
2001.
On Lie derivations of Lie ideals of prime algebras.
Israel Journal of Mathematics,
Vol. 123,
Issue. 1,
p.
131.
Chebotar, M. A.
Lee, Pjek-Hwee
and
Wong, Tsai-Lien
2002.
A NOTE ON DERIVATIONS, ADDITIVE SUBGROUPS, AND LIE IDEALS OF PRIME RINGS.
Communications in Algebra,
Vol. 30,
Issue. 10,
p.
5011.
Бейдар, Константин Игоревич
Beidar, Konstantin Igorevich
Михалeв, Александр Васильевич
Mikhalev, Aleksandr Vasil'evich
Чеботарь, Михаил Александрович
and
Chebotar, Mikhail Aleksandrovich
2004.
Функциональные тождества в кольцах и их приложения.
Успехи математических наук,
Vol. 59,
Issue. 3,
p.
3.
Yu, Weiyan
and
Zhang, Jianhua
2010.
Nonlinear Lie derivations of triangular algebras.
Linear Algebra and its Applications,
Vol. 432,
Issue. 11,
p.
2953.
Ghahramani, H.
Ghosseiri, M. N.
and
Heidari Zadeh, L.
2019.
On the Lie derivations and generalized Lie derivations of quaternion rings.
Communications in Algebra,
Vol. 47,
Issue. 3,
p.
1215.

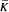 , a derivation
, a derivation  = 0.
= 0.