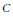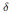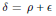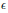Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beidar, K. I.
and
Chebotar, M. A.
2001.
On Lie derivations of Lie ideals of prime algebras.
Israel Journal of Mathematics,
Vol. 123,
Issue. 1,
p.
131.
Beidar, K.I
Brešar, M
Chebotar, M.A
and
Martindale, W.S
2001.
On Herstein's Lie Map Conjectures, II.
Journal of Algebra,
Vol. 238,
Issue. 1,
p.
239.
Beidar, K. I.
Bres˘ar, M.
and
Chebotar, M. A.
2002.
FUNCTIONAL IDENTITIES REVISED: THE FRACTIONAL AND THE STRONG DEGREE.
Communications in Algebra,
Vol. 30,
Issue. 2,
p.
935.
Chebotar, M. A.
Lee, Pjek-Hwee
and
Wong, Tsai-Lien
2002.
A NOTE ON DERIVATIONS, ADDITIVE SUBGROUPS, AND LIE IDEALS OF PRIME RINGS.
Communications in Algebra,
Vol. 30,
Issue. 10,
p.
5011.
Beidar, K. I.
Bresˇar, M.
and
Chebotar, M. A.
2002.
FUNCTIONAL IDENTITIES WITH r-INDEPENDENT COEFFICIENTS.
Communications in Algebra,
Vol. 30,
Issue. 12,
p.
5725.
Beidar, K.I.
Brešar, M.
Chebotar, M.A.
and
Martindale, W.S.
2002.
On Herstein's Lie Map Conjectures, III.
Journal of Algebra,
Vol. 249,
Issue. 1,
p.
59.
Breˇsar, Matej
2004.
COMMUTING MAPS: A SURVEY.
Taiwanese Journal of Mathematics,
Vol. 8,
Issue. 3,
Beidar, K. I.
and
Lin, Ying-Fen
2005.
MAPS CHARACTERIZED BY ACTION ON LIE ZERO PRODUCTS.
Communications in Algebra,
Vol. 33,
Issue. 8,
p.
2697.
Lu, Fangyan
2006.
Lie derivations of certain CSL algebras.
Israel Journal of Mathematics,
Vol. 155,
Issue. 1,
p.
149.
Xiuping, Xiuping
and
Lu, Fangyan
2008.
MAPS PRESERVING LIE PRODUCT ON B(X).
Taiwanese Journal of Mathematics,
Vol. 12,
Issue. 3,
Liao, Ping-Bao
and
Liu, Cheng-Kai
2009.
On generalized Lie derivations of Lie ideals of prime algebras.
Linear Algebra and its Applications,
Vol. 430,
Issue. 4,
p.
1236.
Lu, Fangyan
and
Liu, Benhong
2010.
Lie derivable maps on B(X).
Journal of Mathematical Analysis and Applications,
Vol. 372,
Issue. 2,
p.
369.
Chen, Lin
Lu, Fangyan
and
Wang, Ting
2013.
Local and 2-Local Lie Derivations of Operator Algebras on Banach Spaces.
Integral Equations and Operator Theory,
Vol. 77,
Issue. 1,
p.
109.