Article contents
Lefschetz Numbers for C*-Algebras
Published online by Cambridge University Press: 20 November 2018
Abstract
Using Poincaré duality, we obtain a formula of Lefschetz type that computes the Lefschetz number of an endomorphism of a separable nuclear 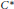 ${{C}^{*}}$ -algebra satisfying Poincaré duality and the Kunneth theorem. (The Lefschetz number of an endomorphism is the graded trace of the induced map on
${{C}^{*}}$ -algebra satisfying Poincaré duality and the Kunneth theorem. (The Lefschetz number of an endomorphism is the graded trace of the induced map on  $\text{K}$ -theory tensored with
$\text{K}$ -theory tensored with  $\mathbb{C}$ , as in the classical case.) We then examine endomorphisms of Cuntz–Krieger algebras
$\mathbb{C}$ , as in the classical case.) We then examine endomorphisms of Cuntz–Krieger algebras 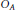 ${{O}_{A}}$ . An endomorphism has an invariant, which is a permutation of an infinite set, and the contracting and expanding behavior of this permutation describes the Lefschetz number of the endomorphism. Using this description, we derive a closed polynomial formula for the Lefschetz number depending on the matrix A and the presentation of the endomorphism.
${{O}_{A}}$ . An endomorphism has an invariant, which is a permutation of an infinite set, and the contracting and expanding behavior of this permutation describes the Lefschetz number of the endomorphism. Using this description, we derive a closed polynomial formula for the Lefschetz number depending on the matrix A and the presentation of the endomorphism.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
- 6
- Cited by

