Article contents
Kirszbraun’s Theorem via an Explicit Formula
Published online by Cambridge University Press: 29 April 2020
Abstract
Let 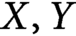 $X,Y$ be two Hilbert spaces, let E be a subset of
$X,Y$ be two Hilbert spaces, let E be a subset of 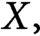 $X,$ and let
$X,$ and let 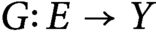 $G\colon E \to Y$ be a Lipschitz mapping. A famous theorem of Kirszbraun’s states that there exists
$G\colon E \to Y$ be a Lipschitz mapping. A famous theorem of Kirszbraun’s states that there exists 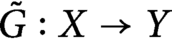 $\tilde {G} : X \to Y$ with
$\tilde {G} : X \to Y$ with 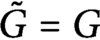 $\tilde {G}=G$ on E and
$\tilde {G}=G$ on E and 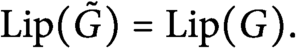 $ \operatorname {\mathrm {Lip}}(\tilde {G})= \operatorname {\mathrm {Lip}}(G).$ In this note we show that in fact the function
$ \operatorname {\mathrm {Lip}}(\tilde {G})= \operatorname {\mathrm {Lip}}(G).$ In this note we show that in fact the function 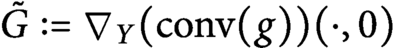 $\tilde {G}:=\nabla _Y( \operatorname {\mathrm {conv}} (g))( \cdot , 0)$, where
$\tilde {G}:=\nabla _Y( \operatorname {\mathrm {conv}} (g))( \cdot , 0)$, where 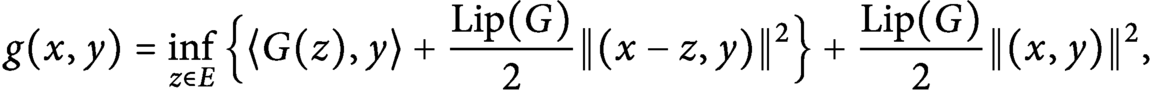
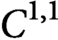 $C^{1,1}$ strongly convex functions.
$C^{1,1}$ strongly convex functions.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
D. Azagra and C. Mudarra were partially supported by Grant MTM2015-65825-P and by the Severo Ochoa Program for Centres of Excellence in R & D (Grant SEV-2015-0554).
References
- 8
- Cited by


