No CrossRef data available.
Article contents
Infinitesimal Isometries on Compact Manifolds
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let X denote a non-vanishing infinitesimal isometry on a compact Riemannian manifold Mn . Let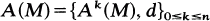 
denote the deRham complex of M. We write i(X) for the operator of interior product, and L(X) the Lie derivative on the elements of A(M). We define E(M) = {u ∈ A(M)| i(X)u = 0, L(X)u= 0}.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1980
References
1.
Borel, A., Seminar on transformation groups.
Ann. of Math. Studies #46. Princeton Univ. Press 1960.Google Scholar
2.
Bredon, G., Introduction to compact transformation groups.
Academic Press, New York
1972.Google Scholar
3.
Connor, P. E. and Floyd, E. E., Orbit spaces of circle groups of transformation.
Ann. of Math.
67 (1958), 90-98.Google Scholar
4.
Dold, A., Lectures on algebraic topology.
Springer-Verlag, New York-Heidelberg-Berlin
1972.Google Scholar
5.
Greub, W., Halperin, S., and Vanstone, R., Connections, curvature, and cohomology. Vol II, Academic Press, New York-London
1973.Google Scholar
6.
Illman, S., Smooth equivariant triangulation of G-manifolds for G a finite group.
Math. Ann.
233 (1978), 199-220.Google Scholar
7.
Liang, C. C., Vector fields on V-manifolds, and locally free G
x ^-actions on manifolds. Indiana Univ. Math. J.
27 (1978), 349-352.Google Scholar
8.
Liang, C. C., Vector fields orthogonal to a non-vanishing infinitesimal isometry.
Proc. Amer. Math. Soc.
75 (1979), 145-148.Google Scholar
You have
Access