No CrossRef data available.
Article contents
The Hausdorff Moment Problem
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Suppose throughout that
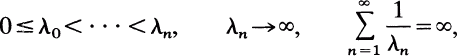
and that {μn}(n≥ 0) is a sequence of real numbers. The (generalized) Hausdorff moment problem is to determine necessary and sufficient conditions for there to be a function x in some specified class satisfying
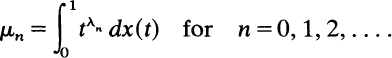 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1978
References
3.
Berman, D. L., Application of interpolator polynomial operators to solve the moment problem,
Ukrain Math. Ž.
14 (1963), 184-190.Google Scholar
4.
Endl, K., On systems of linear inequalities in infinitely many variables and generalized Hausdorff means,
Math. Z.
82 (1963), 1-7.Google Scholar
7.
Hausdorff, F., Momentprobleme fur ein eindliches Interval,
Math. Z.
16 (1923), 220-248.Google Scholar
8.
Hildebrandt, T. H., On the moment problem for a finite interval,
Bull. A.M.S.
38 (1932), 269-270.Google Scholar
10.
Leviatan, D., Some moment problems in a finite interval,
Can. J. Math.
20 (1968), 960-966.Google Scholar
12.
Schoenberg, I. J., On finite rowed systems of linear inequalities in infinitely many variables,
Trans. A.M.S.
34 (1932) 594-619.Google Scholar

