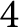Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harris, Robert
Joshi, Amey
Doug Park, B.
and
Poddar, Mainak
2023.
Abelian branched covers of rational surfaces.
Advances in Geometry,
Vol. 23,
Issue. 3,
p.
401.
Akhmedov, Anar
Sakallı, Sümeyra
and
Yeung, Sai-Kee
2024.
Complex Ball Quotients and New Symplectic $4$-manifolds with Nonnegative Signatures.
Taiwanese Journal of Mathematics,
Vol. 28,
Issue. 1,
Park, B. Doug
2024.
Slope inequalities for the geography problem of nonspin symplectic 4-manifolds.
Topology and its Applications,
Vol. 344,
Issue. ,
p.
108813.