Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Singh, T.
and
Rai, L. N.
1983.
Scalar-tensor theories of gravitation: Foundations and prospects.
General Relativity and Gravitation,
Vol. 15,
Issue. 9,
p.
875.

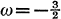 and
and 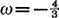 . Peters [3, 4] has shown that when
. Peters [3, 4] has shown that when 