Article contents
A Generalization of a Theorem of Boyd and Lawton
Published online by Cambridge University Press: 20 November 2018
Abstract.
The Mahler measure of a nonzero  $n$ -variable polynomial
$n$ -variable polynomial  $P$ is the integral of
$P$ is the integral of 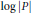 $\log \,\left| P \right|$ on the unit
$\log \,\left| P \right|$ on the unit  $n$ -torus. A result of Boyd and Lawton says that the Mahler measure of a multivariate polynomial is the limit of Mahler measures of univariate polynomials. We prove the analogous result for different extensions of Mahler measure such as generalized Mahler measure (integrating the maximum of
$n$ -torus. A result of Boyd and Lawton says that the Mahler measure of a multivariate polynomial is the limit of Mahler measures of univariate polynomials. We prove the analogous result for different extensions of Mahler measure such as generalized Mahler measure (integrating the maximum of 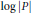 $\log \,\left| P \right|$ for possibly different
$\log \,\left| P \right|$ for possibly different 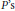 ${{P}^{'}}\text{s}$ ), multiple Mahler measure (involving products of
${{P}^{'}}\text{s}$ ), multiple Mahler measure (involving products of 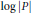 $\log \,\left| P \right|$ for possibly different
$\log \,\left| P \right|$ for possibly different 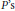 ${{P}^{'}}\text{s}$ ), and higher Mahler measure (involving
${{P}^{'}}\text{s}$ ), and higher Mahler measure (involving 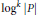 ${{\log }^{k}}\,\left| P \right|$ ).
${{\log }^{k}}\,\left| P \right|$ ).
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 4
- Cited by

