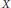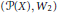Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ohta, Shin-ichi
and
Takatsu, Asuka
2011.
Displacement convexity of generalized relative entropies.
Advances in Mathematics,
Vol. 228,
Issue. 3,
p.
1742.
Ohta, Shin-ichi
and
Sturm, Karl-Theodor
2012.
Non-Contraction of Heat Flow on Minkowski Spaces.
Archive for Rational Mechanics and Analysis,
Vol. 204,
Issue. 3,
p.
917.
Ambrosio, Luigi
Gigli, Nicola
and
Savaré, Giuseppe
2013.
Analysis and Numerics of Partial Differential Equations.
Vol. 4,
Issue. ,
p.
63.
Ohta, Shin-Ichi
2014.
Optimal Transport.
p.
145.
Ohta, Shin-ichi
2014.
On the Curvature and Heat Flow on Hamiltonian Systems.
Analysis and Geometry in Metric Spaces,
Vol. 2,
Issue. 1,
Juillet, Nicolas
2014.
Diffusion by optimal transport in Heisenberg groups.
Calculus of Variations and Partial Differential Equations,
Vol. 50,
Issue. 3-4,
p.
693.
Ambrosio, Luigi
Gigli, Nicola
and
Savaré, Giuseppe
2014.
Metric measure spaces with Riemannian Ricci curvature bounded from below.
Duke Mathematical Journal,
Vol. 163,
Issue. 7,
Ambrosio, Luigi
Brué, Elia
and
Semola, Daniele
2021.
Lectures on Optimal Transport.
Vol. 130,
Issue. ,
p.
229.
Dolera, Emanuele
2022.
Asymptotic Efficiency of Point Estimators in Bayesian Predictive Inference.
Mathematics,
Vol. 10,
Issue. 7,
p.
1136.
Ambrosio, Luigi
Brué, Elia
and
Semola, Daniele
2024.
Lectures on Optimal Transport.
Vol. 169,
Issue. ,
p.
239.
Dolera, Emanuele
Favaro, Stefano
and
Mainini, Edoardo
2024.
Strong posterior contraction rates via Wasserstein dynamics.
Probability Theory and Related Fields,
Vol. 189,
Issue. 1-2,
p.
659.