Hostname: page-component-7f64f4797f-l842n Total loading time: 0 Render date: 2025-11-04T14:08:45.796Z Has data issue: false hasContentIssue false
  • English
  • Français

The f-Chromatic Index of a Graph Whose f-Core Has Maximum Degree 2

Published online by Cambridge University Press:  20 November 2018

S. Akbari ,
M. Chavooshi ,
M. Ghanbari  and
S. Zare
S. Akbari
Affiliation:
Department of Mathematical Sciences, Sharif University of Technology, Tehran, Iran e-mail: s_akbari@sharif.edu
M. Chavooshi
Affiliation:
School of Mathematics, Institute for Studies in Theoretical Physics and Mathematics, P.O. Box 19395-5746, Tehran, Iran e-mail: chavooshi.m@gmail.com; marghanbari@gmail.com
M. Ghanbari
Affiliation:
School of Mathematics, Institute for Studies in Theoretical Physics and Mathematics, P.O. Box 19395-5746, Tehran, Iran e-mail: chavooshi.m@gmail.com; marghanbari@gmail.com
S. Zare
Affiliation:
Department of Mathematical Sciences, Amirkabir University of Technology, Tehran, Iran e-mail: sa_zare_f@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $G$ be a graph. The minimum number of colors needed to color the edges of $G$ is called the chromatic index of $G$ and is denoted by 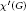$X'\left( G \right)$ . It is well known that 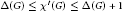$\Delta \left( G \right)\,\le \,\mathcal{X}'\left( G \right)\,\le \Delta \left( G \right)\,+\,1$ , for any graph $G$ , where 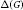$\Delta \left( G \right)$ denotes the maximum degree of $G$ . A graph $G$ is said to be class 1 if 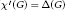${\mathcal{X}}'\left( G \right)\,=\,\Delta \left( G \right)$ and class 2 if 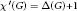${\mathcal{X}}'\left( G \right)\,=\,\Delta \left( G \right)\,+\,1$ . Also, ${{G}_{\Delta }}$ is the induced subgraph on all vertices of degree 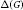$\Delta \left( G \right)$ . Let 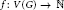$f:\,V\left( G \right)\,\to \mathbb{N}$ be a function. An $f$ -coloring of a graph $G$ is a coloring of the edges of 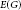$E\left( G \right)$ such that each color appears at each vertex 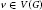$v\,\in \,V\left( G \right)$ at most 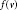$f\left( v \right)$ times. The minimum number of colors needed to $f$ -color $G$ is called the $f$ -chromatic index of $G$ and is denoted by 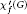${{{\mathcal{X}}'}_{f}}\left( G \right)$ . It was shown that for every graph $G,\,{{\Delta }_{f}}\,\left( G \right)\,\le \,{{\mathcal{X}}^{\prime }}_{f}\left( G \right)\,\le \,{{\Delta }_{f}}\,\left( G \right)\,+\,1$ , where 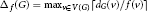${{\Delta }_{f}}\left( G \right)\,=\,{{\max }_{v\in \left( G \right)}}\,\left\lceil {{{d}_{G}}\left( v \right)}/{f\left( v \right)}\; \right\rceil $ . A graph $G$ is said to be $f$ -class 1 if ${{\mathcal{X}}^{\prime }}_{f}\left( G \right)\,=\,{{\Delta }_{f}}\left( G \right)$ , and $f$ -class 2, otherwise. Also, 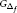${{G}_{{{\Delta }_{f}}}}$ is the induced subgraph of $G$ on 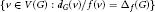$\left\{ v\,\in \,V\left( G \right)\,:\,{{{d}_{G}}\left( V \right)}/{f\left( v \right)}\;\,=\,{{\Delta }_{f}}\left( G \right) \right\}$ . Hilton and Zhao showed that if ${{G}_{\Delta }}$ has maximum degree two and $G$ is class 2, then $G$ is critical, ${{G}_{\Delta }}$ is a disjoint union of cycles and 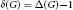$\delta \left( G \right)\,=\,\Delta \left( G \right)-1$ , where 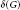$\delta \left( G \right)$ denotes the minimum degree of $G$ , respectively. In this paper, we generalize this theorem to $f$ -coloring of graphs. Also, we determine the $f$ -chromatic index of a connected graph $G$ with 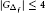$\left| {{G}_{{{\Delta }_{f}}}} \right|\,\le \,4$ .

Keywords

05C1505C38ƒ-coloringƒ-coreƒ-class 1

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 449 - 458
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Akbari, S., Cariolaro, D., Chavooshi, M., Ghanbari, M., and Zare, S., Some criteria for a graph to be class 1. Discrete Math. 312 (2012), 2593–2598. http://dx.doi.org/10.1016/j.disc.2011.09.035 Google Scholar
[2] Chetwynd, A. G. and Hilton, A.J.W., Regular graphs of high degree are 1-factorizable. Proc. London Math. Soc. 50 (1985), 193–196. http://dx.doi.org/10.1112/plms/s3-50.2.193 Google Scholar
[3] Chetwynd, A. G. and Hilton, A.J.W., The chromatic index of graphs with at most four vertices of maximum degree. Congr. Numer. 43 (1984), 221–248.Google Scholar
[4] Coffman, E. G., Garey, M. R., Johnson, D. S., and LaPaugh, A. S., Scheduling file transfers. SIAM J. Comput. 14 (1985), 744–780. http://dx.doi.org/10.1137/0214054 Google Scholar
[5] Hakimi, S. L. and Kariv, O., A generalization of edge-coloring in graphs. J. Graph Theory 10 (1986), 139–154. http://dx.doi.org/10.1002/jgt.3190100202 Google Scholar
[6] Hilton, A. J.W. and Zhao, C., The chromatic index of a graph whose core has maximum degree two. Discrete Math. 101 (1992), 135–147. http://dx.doi.org/10.1016/0012-365X(92)90598-A Google Scholar
[7] Krawczyk, H. and Kubale, M., An approximation algorithm for diagnostic test scheduling in multicomputer systems. IEEE Trans. Comput. 34 (1985), 869–872.Google Scholar
[8] Liu, G., Hou, J., and Cai, J., Some results about f -critical graphs. Published online inWiley InterScience, 2007). http://dx.doi.org/10.1002/net.20190 Google Scholar
[9] Nakano, S., Nishizeki, T., and Saito, N., On the f -coloring of multigraphs. IEEE Trans Circuits Systems 35 (1988), 345–353. http://dx.doi.org/10.1109/31.1747 Google Scholar
[10] Vizing, V. G., The chromatic class of a multigraph. Kibernetika 3 (1965), 29–39.Google Scholar
[11] Zhang, X. and Liu, G., A class of graphs of f -class 1. In: International Conference on Computational Science (ICCS 2007, Beijing, China), LNCS 4489 (2007), 362–369.Google Scholar
[12] Zhang, X. and Liu, G., Some graphs of class 1 for f -colorings. Appl. Math. Letters 21 (2008), 23–39. http://dx.doi.org/10.1016/j.aml.2007.02.009 Google Scholar
[13] Zhang, X., Wang, J., and Liu, G., The classification of regular graphs on f -colorings. Ars. Combin. 86 (2008), 273–280.Google Scholar