Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-11T09:52:53.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Examples of exponential bases on union of intervals

Part of: Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  15 May 2023

Oleg Asipchuk  and
Vladyslav Drezels
Oleg Asipchuk*
Affiliation:
Department of Mathematics and Statistics, Florida International University, Miami, FL 33199, USA e-mail: vdrez001@fiu.edu
Vladyslav Drezels
Affiliation:
Department of Mathematics and Statistics, Florida International University, Miami, FL 33199, USA e-mail: vdrez001@fiu.edu
*
e-mail: aasip001@fiu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we construct explicit exponential bases of unions of segments of total measure one. Our construction applies to finite or infinite unions of segments, with some conditions on the gaps between them. We also construct exponential bases on finite or infinite unions of cubes in 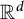$\mathbb {R}^d$ and prove a stability result for unions of segments that generalize Kadec’s $\frac 14$-theorem.

Keywords

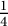Exponential basesRiesz basesRiesz constantsframesKadec stability theorem

MSC classification

Primary: 42C15: General harmonic expansions, frames
Secondary: 42C30: Completeness of sets of functions
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 4 , December 2023 , pp. 1296 - 1312
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of this project started during the Summer 2022 REU program “AMRPU FIU” that took place at the Department of Mathematics and Statistics, Florida International University, which was supported by the NSA grant H982302210016 and the NSF (REU Site) grant DMS-2050971.

References

Avdonin, S. A., On the question of Riesz bases of exponential functions in ${L}^2$ $.$ Vestn. Leningr. Univ. No. 13 Mat. Meh. Astron. Vyp. 3 (1974), 5–12, 154.Google Scholar
Balan, R., Stability theorems for Fourier frames and wavelet Riesz bases. Dedicated to the memory of Richard J. Duffin . J. Fourier Anal. Appl. 3(1997), no. 5, 499–504.CrossRefGoogle Scholar
Bose, D., Kumar, C. P. A., Krishnan, R., and Madan, S., On Fuglede’s conjecture for three intervals . Online J. Anal. Comb. 5(2010), Article no. 1, 24 ppGoogle Scholar
De Carli, L., Concerning exponential bases on multi-rectangles of ${R}^d$ . In: Topics in classical and modern analysis: in memory of Yingkang Hu, Applied and Numerical Harmonic Analysis, Birkhäuser/Springer, Cham, 2019, pp. 65–85.CrossRefGoogle Scholar
De Carli, L. and Kumar, A., Exponential bases on two dimensional trapezoids . Proc. Amer. Math. Soc. 143(2015), no. 7, 2893–2903.CrossRefGoogle Scholar
De Carli, L., Mizrahi, A., and Tepper, A., Three problems on exponential bases . Can. Math. Bull. 62(2019), no. 1, 55–70.CrossRefGoogle Scholar
Fogel, L. J., A note on the sampling theorem . IRE Trans. Inform. Theory 1(1955), 47–48.CrossRefGoogle Scholar
Heil, C., A basis theory primer, expanded edition, Applied and Numerical Harmonic Analysis, Birkhäuser/Springer, New York, 2011, xxvi + 534 pp.CrossRefGoogle Scholar
Iosevich, A. and Kolountzakis, M. N., Periodicity of the spectrum in dimension one . Anal. PDE 6(2013), no. 4, 819–827.CrossRefGoogle Scholar
Kolountzakis, M. N., The study of translational tiling with Fourier analysis . In: Fourier analysis and convexity, Applied and Numerical Harmonic Analysis, Birkhäuser, Boston, MA, 2004, pp. 131–187.CrossRefGoogle Scholar
Kozma, G. and Nitzan, S., Combining Riesz bases in ${R}^d$ $.$ Invent. Math. 199(2015), no. 1, 267–285.CrossRefGoogle Scholar
Laba, I., Fuglede’s conjecture for a union of two intervals . Proc. Amer. Math. Soc. 129(2001), no. 10, 2965–2972.CrossRefGoogle Scholar
Landau, H. J., Necessary density conditions for sampling and interpolation of certain entire functions . Acta Math. 117(1967), 37–52.CrossRefGoogle Scholar
Lev, N., Riesz bases of exponentials on multiband spectra . Proc. Amer. Math. Soc. 140(2012), no. 9, 3127–3132.CrossRefGoogle Scholar
Lev, N. and Matolcsi, M., The Fuglede conjecture for convex domains is true in all dimensions . Acta Math. 228(2022), no. 2, 385–420.CrossRefGoogle Scholar
Nitzan, S., Olevskii, A., and Ulanovskii, A., Exponential frames on unbounded sets . Proc. Amer. Math. Soc. 144(2016), no. 1, 109–118.CrossRefGoogle Scholar
Paley, R. E. A. C. and Wiener, N., Fourier transforms in the complex domain, American Mathematical Society Colloquium Publications, 19, American Mathematical Society, Providence, RI, 1987, x + 184 pp. Reprint of the 1934 originalGoogle Scholar
Pavlov, B. S., The basis property of a system of exponentials and the condition of Muckenhoupt. Dokl. Akad. Nauk SSSR 247(1979), no. 1, 37–40 (in Russian).Google Scholar
Pfander, G., Shauna, R., and Walnut, D., Exponential bases for partitions of intervals. Preprint, 2021. arXiv:2109.04441 Google Scholar
Seip, K., On the connection between exponential bases and certain related sequences in ${\mathrm{L}}^2\left(-\pi, \pi \right)$ . J. Funct. Anal. 130(1995), no. 1, 131–160.CrossRefGoogle Scholar
Selvan, A. A. and Ghosh, R., Sampling with derivatives in periodic shift-invariant spaces . Numer. Funct. Anal. Optim. 43(2022), no. 13, 1591–1615.CrossRefGoogle Scholar
Stein, E. M. and Shakarchi, R., Fourier analysis, Princeton University Press, Princeton, NJ, 2003.Google Scholar
Sun, W. and Zhou, X., On the stability of multivariate trigonometric systems . J. Math. Anal. Appl. 235(1999), no. 1, 159–167.CrossRefGoogle Scholar
Young, R. M., An introduction to nonharmonic Fourier series, Pure and Applied Mathematics, 93, Academic Press (Harcourt Brace Jovanovich), New York–London, 1980, x + 246 pp.Google Scholar