No CrossRef data available.
Article contents
Even Covering Properties and Somewhat Normal Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
A topological space X is said to be somewhat normal provided that for each open cover 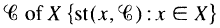 is a normal cover of X. We show that a completely regular somewhat normal space need not be normal, thereby answering a question of W. M. Fleischman. We note that a collectionwise normal somewhat normal space need not be almost 2-fully normal, as had previously been asserted, and that neither the perfect image nor the perfect preimage of a somewhat normal space has to be somewhat normal.
is a normal cover of X. We show that a completely regular somewhat normal space need not be normal, thereby answering a question of W. M. Fleischman. We note that a collectionwise normal somewhat normal space need not be almost 2-fully normal, as had previously been asserted, and that neither the perfect image nor the perfect preimage of a somewhat normal space has to be somewhat normal.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1986
References
1.
Asanov, M.W., Properties that are close to paracompactness, Math. Zapeski
9 (1975), pp. 3—9. (Russian)Google Scholar
2.
Cohen, H.J., Sur un problème de M. Dieudonné, C.R. Acad. Sri., Paris
234 (1952), pp. 290–292.Google Scholar
3.
van Douwen, E., Hausdorff gaps and a nice countably paracompact nonnormal space, Topology Proc.
1 (1976), pp. 239–242.Google Scholar
4.
Engelking, R., General Topology, Monografie Mat.
60, Polish Scientific Publishers, Warsaw, 1977.Google Scholar
5.
Fleischman, W.M., A new extension of countable compactness, Fund. Math.
67 (1970), pp. 1—9.Google Scholar
6.
Hart, K.P., Strong collectionwise normality and M. E. Rudin’ s Dowker space, Proc. Amer. Math. Soc.
83 (1981), pp. 802–806.Google Scholar
7.
Kljusin, V.L., On spaces with regularly refinable coverings, Dokl. Akad. Nauk SSSR
204 (1972), pp. 782–783. Soviet Math. Dokl. 13 (1972), pp. 740-742.Google Scholar
8.
Mack, J., On a class of countably paracompact spaces, Proc. Amer. Math. Soc.
16 (1965), pp. 467–472.Google Scholar
9.
Mack, J.E. and Johnson, D.G., The Dedekind completion of C(X), Pacific J. Math.
20 (1967), pp. 231–243.Google Scholar
10.
Michael, E., Point-finite and locally finite coverings, Canad. J. Math.
7 (1955), pp. 275–279.Google Scholar
11.
Moore, R.L., Foundations of Point-set Theory, Amer. Math. Soc. Publ. No. 13, revised edition, 1962.Google Scholar
12.
Shapiro, H.L. and Smith, F.A., Even covers and collectionwise normal spaces, Canad. J. Math.
30 (1978), pp. 466–473.Google Scholar
13.
Shapiro, H.L. and Smith, F.A., Paracompactness in uniform spaces, Topology Proc.
3 (1978), pp. 179–197.Google Scholar
14.
Shapiro, H.L. and Smith, F.A., Neighborhoods of the diagonal and strong normality properties, Proc. Amer. Math. Soc.
71 (1978), pp. 329–333.Google Scholar

