Article contents
Estimates of Henstock-Kurzweil Poisson Integrals
Published online by Cambridge University Press: 20 November 2018
Abstract
If 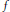 $f$ is a real-valued function on
$f$ is a real-valued function on 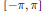 $\left[ -\pi ,\,\pi\right]$ that is Henstock-Kurzweil integrable, let
$\left[ -\pi ,\,\pi\right]$ that is Henstock-Kurzweil integrable, let 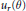 ${{u}_{r}}(\theta )$ be its Poisson integral. It is shown that
${{u}_{r}}(\theta )$ be its Poisson integral. It is shown that 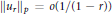 ${{\left\| {{u}_{r}} \right\|}_{p}}\,=\,o\left( 1/\left( 1-r \right) \right)$ as
${{\left\| {{u}_{r}} \right\|}_{p}}\,=\,o\left( 1/\left( 1-r \right) \right)$ as 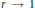 $r\,\to \,1$ and this estimate is sharp for
$r\,\to \,1$ and this estimate is sharp for 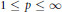 $1\,\le \,p\,\le \,\infty $ . If
$1\,\le \,p\,\le \,\infty $ . If  $\mu $ is a finite Borel measure and
$\mu $ is a finite Borel measure and 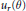 ${{u}_{r}}(\theta )$ is its Poisson integral then for each
${{u}_{r}}(\theta )$ is its Poisson integral then for each 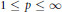 $1\,\le \,p\,\le \,\infty $ the estimate
$1\,\le \,p\,\le \,\infty $ the estimate 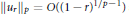 ${{\left\| {{u}_{r}} \right\|}_{p}}\,=\,O\left( {{\left( 1-r \right)}^{1/p-1}} \right)$ as
${{\left\| {{u}_{r}} \right\|}_{p}}\,=\,O\left( {{\left( 1-r \right)}^{1/p-1}} \right)$ as 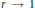 $r\,\to \,1$ is sharp. The Alexiewicz norm estimates
$r\,\to \,1$ is sharp. The Alexiewicz norm estimates 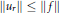 $\left\| {{u}_{r}} \right\|\,\le \,\left\| f \right\|$
$\left\| {{u}_{r}} \right\|\,\le \,\left\| f \right\|$ 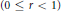 $\left( 0\,\le \,r\,<\,1 \right)$ and
$\left( 0\,\le \,r\,<\,1 \right)$ and 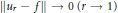 $\left\| {{u}_{r}}-f \right\|\,\to 0\left( r\to 1 \right)$ hold. These estimates lead to two uniqueness theorems for the Dirichlet problem in the unit disc with Henstock-Kurzweil integrable boundary data. There are similar growth estimates when
$\left\| {{u}_{r}}-f \right\|\,\to 0\left( r\to 1 \right)$ hold. These estimates lead to two uniqueness theorems for the Dirichlet problem in the unit disc with Henstock-Kurzweil integrable boundary data. There are similar growth estimates when 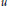 $u$ is in the harmonic Hardy space associated with the Alexiewicz norm and when
$u$ is in the harmonic Hardy space associated with the Alexiewicz norm and when 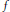 $f$ is of bounded variation.
$f$ is of bounded variation.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005
References
- 3
- Cited by

