Article contents
Essential Dimension, Symbol Length and 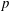 $p$-rank
$p$-rank
Published online by Cambridge University Press: 04 February 2020
Abstract
We prove that the essential dimension of central simple algebras of degree 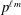 $p^{\ell m}$ and exponent
$p^{\ell m}$ and exponent 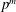 $p^{m}$ over fields
$p^{m}$ over fields 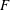 $F$ containing a base-field
$F$ containing a base-field 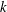 $k$ of characteristic
$k$ of characteristic 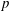 $p$ is at least
$p$ is at least 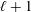 $\ell +1$ when
$\ell +1$ when 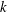 $k$ is perfect. We do this by observing that the
$k$ is perfect. We do this by observing that the  $p$-rank of
$p$-rank of 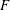 $F$ bounds the symbol length in
$F$ bounds the symbol length in 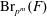 $\text{Br}_{p^{m}}(F)$ and that there exist indecomposable
$\text{Br}_{p^{m}}(F)$ and that there exist indecomposable 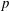 $p$-algebras of degree
$p$-algebras of degree 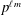 $p^{\ell m}$ and exponent
$p^{\ell m}$ and exponent 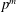 $p^{m}$. We also prove that the symbol length of the Kato-Milne cohomology group
$p^{m}$. We also prove that the symbol length of the Kato-Milne cohomology group 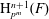 $\text{H}_{p^{m}}^{n+1}(F)$ is bounded from above by
$\text{H}_{p^{m}}^{n+1}(F)$ is bounded from above by 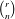 $\binom{r}{n}$ where
$\binom{r}{n}$ where  $r$ is the
$r$ is the 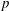 $p$-rank of the field, and provide upper and lower bounds for the essential dimension of Brauer classes of a given symbol length.
$p$-rank of the field, and provide upper and lower bounds for the essential dimension of Brauer classes of a given symbol length.
Keywords
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
- 1
- Cited by


