No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
A well-known theorem of Schütte (1963) gives a sharp lower bound for the ratio of the maximum and minimum distances between 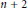 $n\,+\,2$ points in
$n\,+\,2$ points in  $n$-dimensional Euclidean space. In this note we adapt Bárány’s elegant proof (1994) of this theorem to the space
$n$-dimensional Euclidean space. In this note we adapt Bárány’s elegant proof (1994) of this theorem to the space 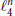 $\ell _{4}^{n}$. This gives a new proof that the largest cardinality of an equilateral set in
$\ell _{4}^{n}$. This gives a new proof that the largest cardinality of an equilateral set in 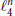 $\ell _{4}^{n}$ is
$\ell _{4}^{n}$ is 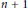 $n\,+\,1$ and gives a constructive bound for an interval
$n\,+\,1$ and gives a constructive bound for an interval  $\left( 4\,-\,{{\varepsilon }_{n}},\,4\,+\,{{\varepsilon }_{n}} \right)$ of values of
$\left( 4\,-\,{{\varepsilon }_{n}},\,4\,+\,{{\varepsilon }_{n}} \right)$ of values of 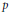 $p$ close to 4 for which it is known that the largest cardinality of an equilateral set in
$p$ close to 4 for which it is known that the largest cardinality of an equilateral set in 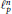 $\ell _{p}^{n}$ is
$\ell _{p}^{n}$ is 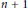 $n\,+\,1$.
$n\,+\,1$.