No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
A space X is a D-space if, for every neighborhood assignment f there is a closed discrete set D such that 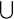 f(D) = X. In this paper we give some necessary conditions and some sufficient conditions for a resolution of a topological space to be a D-space. In particular, if a space X is resolved at each x ∊ X into a D-space Yx by continuous mappings fx: X − {x} → Yx, then the resolution is a D-space if and only if
f(D) = X. In this paper we give some necessary conditions and some sufficient conditions for a resolution of a topological space to be a D-space. In particular, if a space X is resolved at each x ∊ X into a D-space Yx by continuous mappings fx: X − {x} → Yx, then the resolution is a D-space if and only if 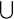 {x} × Bd(Yx) is a D-space.
{x} × Bd(Yx) is a D-space.