Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-11T10:36:42.681Z Has data issue: false hasContentIssue false
  • English
  • Français

Domains of Injective Holomorphy

Published online by Cambridge University Press:  20 November 2018

P. M. Gauthier  and
V. Nestoridis
P. M. Gauthier
Affiliation:
Département de Mathématiques et statistiques, Université de Montréal, Montreal, QC H3C 3J7e-mail: gauthier@dms.UMontreal.ca
V. Nestoridis
Affiliation:
Department of Mathematics, University of Athens, Panepistimioupolis GR-157 84, Athens, Greecee-mail: vnestor@math.uoa.gr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A domain 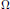$\Omega $ is called a domain of injective holomorphy if there exists an injective holomorphic function 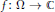$f\,:\,\Omega \,\to \,\mathbb{C}$ that is non-extendable. We give examples of domains that are domains of injective holomorphy and others that are not. In particular, every regular domain 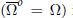$(\overset{\multimap }{\mathop{\Omega }}\,\,=\,\Omega )$ is a domain of injective holomorphy, and every simply connected domain is a domain of injective holomorphy as well.

Keywords

30Exxdomains of holomorphy
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 3 , 01 September 2012 , pp. 509 - 522
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Dienes, P., The Taylor series: an introduction to the theory of functions of a complex variable. Dover Publications, Inc., New York, 1957.Google Scholar
[2] Fuks, B. A., Special chapters in the theory of analytic functions of several complex variables. Translated from the Russian by Jeffrey, A. and Mugibayashi, N.. Translations of Mathematical Monographs, 14, American Mathematical Society, Providence, RI, 1965.Google Scholar
[3] Gauthier, P. M., The Cauchy theorem for domains of arbitrary connectivity on Riemann surfaces. In: Geometric function theory in several complex variables, World Sci. Publ., River Edge, NJ, 2004, pp. 123–142.Google Scholar
[4] Kahane, J.-P., Baire's category theorem and trigonometric series. J. Anal. Math. 80(2000), 143–182. http://dx.doi.org/10.1007/BF02791536 Google Scholar
[5] Nestoridis, V., Non extendable holomorphic functions. Math. Proc. Cambridge Philos. Soc. 139(2005), no. 2, 351–360. http://dx.doi.org/10.1017/S0305004105008728 Google Scholar
[6] Rudin, W., Real and complex analysis. McGraw-Hill, New York-Toronto-London, 1966.Google Scholar
[7] Saks, S. and Zygmund, A., Analytic functions. Second ed., Monografie Matematyczne, 28, Państwowe Wydawnietwo Naukowe, Warsaw, 1965.Google Scholar