Hostname: page-component-5b777bbd6c-7mr9c Total loading time: 0 Render date: 2025-06-22T12:42:09.202Z Has data issue: false hasContentIssue false
  • English
  • Français

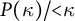Distributivity and base trees for $P(\kappa)/ {\lt} \kappa$

Part of: Set theory

Published online by Cambridge University Press:  07 May 2024

Geoff Galgon
Geoff Galgon*
Affiliation:
Independent, Philadelphia, PA, United States
*
e-mail: geoff@nimbus.solar
Get access Rights & Permissions [Opens in a new window]

Abstract

For 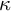$\kappa $ a regular uncountable cardinal, we show that distributivity and base trees for $P(\kappa )/{<}\kappa $ of intermediate height in the cardinal interval 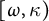$[\omega , \kappa )$ exist in certain models. We also show that base trees of height 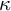$\kappa $ can exist as well as base trees of various heights 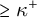$\geq \kappa ^+$ depending on the spectrum of cardinalities of towers in 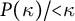$P(\kappa )/{<}\kappa $.

Keywords

Distributivity matrixdistributivity treetree of maximal antichainsgeneralized Baire space

MSC classification

Primary: 03E05: Other combinatorial set theory
Secondary: 03E17: Cardinal characteristics of the continuum
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 4 , December 2024 , pp. 915 - 926
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Balcar, B. and Vopěnka, P., On systems of almost disjoint sets . Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 20(1972), no. 6, 421–424.Google Scholar
Brendle, J., Base matrices of various heights . Canad. Math. Bull. 66(2023), no. 4, 1237–1243. https://doi.org/10.4153/s0008439523000310 CrossRefGoogle Scholar
Fischer, V., Koelbing, M., and Wohofsky, W., The distributivity spectrum of $P(\omega)/\textrm{fin}$ . Preprint, 2022. http://www.logic.univie.ac.at/~koelbingm72/Distributivity.pdf or http://www.logic.univie.ac.at/~vfischer/distributivity07.pdf Google Scholar
Fischer, V., Koelbing, M., and Wohofsky, W., Games on base matrices . Notre Dame J. Form. Log. 64(2023), no. 2, 247–251. https://doi.org/10.1215/00294527-10701451 CrossRefGoogle Scholar
Fischer, V., Koelbing, M., and Wohofsky, W., Refining systems of mad families . Israel J. Math. (2024), 1–44. http://doi.org/10.1007/s11856-024-2626-9Google Scholar
Galgon, G., Trees, refining, and combinatorial characteristics. Doctoral dissertation, UC Irvine, 2016.Google Scholar