No CrossRef data available.
Article contents
Direct Product Decompositions of Elation Groups
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let G be a collineation group of a projective plane π. Let E be the subgroup generated by all elations in G. In the case that π is finite and G fixes no point or line, F. Piper [6; 7] has proved that if G contains certain combinations of perspectivities, then E is isomorphic to 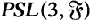 for some finite field g.
for some finite field g.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1977
References
1.
Albert, A. A. and Sandler, R., An introduction to finite projective planes, (Holt, Rinehart and Winston. New York, 1968).Google Scholar
2.
André, J., Über Perspektivitäten in endlichen projektiven Ebenen, Arch. Math.
6 (1955), 29-32.Google Scholar
3.
Coxeter, H. S. M., Projective Geometry, 2nd ed. (University of Toronto Press, Toronto, 1974).Google Scholar
4.
Hering, C., Eine Charakterisierung der endlichen zweidimensionalen projektiven Gruppen, Math. Z.
82 (1963), 152-175.Google Scholar
5.
Hering, C., On shears of translation planes, Abh. Math. Sem. Univ. Hamburg
37 (1972), 258-268.Google Scholar
7.
Piper, F., Collineation groups containing homologies, J. Algebra
6 (1967), 256-269.Google Scholar

