Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kimberling, Clark
1981.
Almost Arithmetic Sequences and Complementary Systems.
The Fibonacci Quarterly,
Vol. 19,
Issue. 5,
p.
426.
Kimberling, Clark
1981.
Fractional Parts (
nr
-
s
), Almost Arithmetic Sequences, And Fibonacci Numbers
.
The Fibonacci Quarterly,
Vol. 19,
Issue. 3,
p.
280.
de Bruijn, N.G.
1981.
Sequences of zeros and ones generated by special production rules.
Indagationes Mathematicae (Proceedings),
Vol. 84,
Issue. 1,
p.
27.
Boshernitzan, M
and
Fraenkel, A.S
1984.
A linear algorithm for nonhomogeneous spectra of numbers.
Journal of Algorithms,
Vol. 5,
Issue. 2,
p.
187.
Aviram, I
1986.
The diffraction spectrum of a general family of linear quasiperiodic arrays.
Journal of Physics A: Mathematical and General,
Vol. 19,
Issue. 16,
p.
3299.
Werman, Michael
Wu, Angela Y.
and
Melter, Robert A.
1987.
Recognition and characterization of digitized curves.
Pattern Recognition Letters,
Vol. 5,
Issue. 3,
p.
207.
de Bruijn, N.G.
1989.
Updown generation of Beatty sequences.
Indagationes Mathematicae (Proceedings),
Vol. 92,
Issue. 4,
p.
385.
Bruckstein, A.M.
1990.
The self-similarity of digital straight lines.
Vol. i,
Issue. ,
p.
485.
Ravenstein, Tony van
Winley, Graham
and
Tognetti, Keith
1990.
Characteristics and the Three Gap Theorem.
The Fibonacci Quarterly,
Vol. 28,
Issue. 3,
p.
204.
Tognetti, Keith
Winley, Graham
and
van Ravenstein, Tony
1990.
Applications of Fibonacci Numbers.
p.
325.
Fraenkel, A. S.
Porta, H.
and
Stolarsky, K. B.
1990.
Analytic Number Theory.
p.
255.
Bunder, Martin
and
Tognetti, Keith
1991.
The Zeckendorf Representation and the Golden Sequence.
The Fibonacci Quarterly,
Vol. 29,
Issue. 3,
p.
217.
Brown, Tom C.
and
Freedman, Allen R.
1991.
Some Sequences Associated with the Golden Ratio.
The Fibonacci Quarterly,
Vol. 29,
Issue. 2,
p.
157.
Siegel, Ralph M.
Tresser, Charles
and
Zettler, George
1992.
A decoding problem in dynamics and in number theory.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 2,
Issue. 4,
p.
473.
Mignosi, Filippo
and
Séébold, Patrice
1993.
Morphismes sturmiens et règles de Rauzy.
Journal de théorie des nombres de Bordeaux,
Vol. 5,
Issue. 2,
p.
221.
Linderbaum, M.
and
Bruckstein, A.
1993.
On recursive, O(N) partitioning of a digitized curve into digital straight segments.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
Vol. 15,
Issue. 9,
p.
949.
Chuan, Wai-fong
1993.
Applications of Fibonacci Numbers.
p.
113.
Crisp, D.
Moran, W.
Pollington, A.
and
Shiue, P.
1993.
Substitution invariant cutting sequences.
Journal de théorie des nombres de Bordeaux,
Vol. 5,
Issue. 1,
p.
123.
Yamashita, Mamoru
1993.
Some Classes of Self-Similar Quasiperiodic Lattices with Uniformity.
Journal of the Physical Society of Japan,
Vol. 62,
Issue. 1,
p.
140.
Berstel, Jean
and
Séébold, Patrice
1993.
Mathematical Foundations of Computer Science 1993.
Vol. 711,
Issue. ,
p.
281.

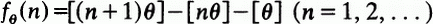 where [x] denotes the greatest integer not exceeding
where [x] denotes the greatest integer not exceeding 