Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Demir, Çağrı
Albaş, Emine
Argaç, Nurcan
and
Fošner, Ajda
2015.
Superderivations with invertible values.
Journal of Algebra and Its Applications,
Vol. 14,
Issue. 02,
p.
1550022.

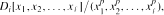 where
where