Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-11T04:03:07.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Completion versus removal of redundancy by perturbation

Part of: Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  05 July 2021

Ole Christensen  and
Marzieh Hasannasab
Ole Christensen*
Affiliation:
DTU Compute, Technical University of Denmark, 2800 Kgs. Lyngby, Denmark
Marzieh Hasannasab
Affiliation:
TU Berlin Institute of Mathematics, Straße des 17. Juni 136, 10623Berlin, Germany e-mail: hasannas@math.tu-berlin.de
*
e-mail: ochr@dtu.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

A sequence 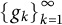$\left \{g_k\right \}_{k=1}^{\infty }$ in a Hilbert space 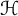${\cal H}$ has the expansion property if each 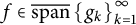$f\in \overline {\text {span}} \left \{g_k\right \}_{k=1}^{\infty }$ has a representation 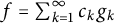$f=\sum _{k=1}^{\infty } c_k g_k$ for some scalar coefficients 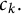$c_k.$ In this paper, we analyze the question whether there exist small norm-perturbations of 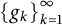$\left \{g_k\right \}_{k=1}^{\infty }$ which allow to represent all 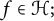$f\in {\cal H};$ the answer turns out to be yes for frame sequences and Riesz sequences, but no for general basic sequences. The insight gained from the analysis is used to address a somewhat dual question, namely, whether it is possible to remove redundancy from a sequence with the expansion property via small norm-perturbations; we prove that the answer is yes for frames 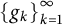$\left \{g_k\right \}_{k=1}^{\infty }$ such that 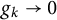$g_k\to 0$ as 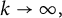$k\to \infty ,$ as well as for frames with finite excess. This particular question is motivated by recent progress in dynamical sampling.

Keywords

FramesRiesz basescompletenessredundancy

MSC classification

Primary: 42C40: Wavelets and other special systems
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 2 , June 2022 , pp. 456 - 465
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldroubi, A., Cabrelli, C., Çakmak, A. F., Molter, U., and Petrosyan, A., Iterative actions of normal operators. J. Funct. Anal. 272(2017), no. 3, 1121–1146.Google Scholar
Aldroubi, A., Cabrelli, C., Molter, U., and Tang, S., Dynamical sampling. Appl. Harm. Anal. Appl. 42(2017), no. 3, 378–401.Google Scholar
Aldroubi, A., Davis, J., and Krishtal, I., Dynamical sampling: time-space trade-off. Appl. Comp. Harm. Anal. 34(2013), no. 3, 495–503.Google Scholar
Balan, R., Casazza, P., Heil, C., and Landau, Z., Deficits and excesses of frames. Adv. Comp. Math. 18(2003), 93–116.CrossRefGoogle Scholar
Casazza, P. G. and Christensen, O., Frames containing a Riesz basis and preservation of this property under perturbation. SIAM J. Math. Anal. 29(1998), no. 1, 266–278.CrossRefGoogle Scholar
Chen, D. Y., Li, L., and Zheng, B. T., Perturbations of frames. Acta Math. Sin. (Engl. Ser.) 30(2014), no. 7, 1089–1108.CrossRefGoogle Scholar
Christensen, O., Frame perturbations. Proc. Amer. Math. Soc. 123(1995), 1217–1220.Google Scholar
Christensen, O., Operators with closed range and perturbation of frames for a subspace. Canad. Math. Bull. 42(1999), no. 1, 37–45.CrossRefGoogle Scholar
Christensen, O., An introduction to frames and Riesz bases. 2nd expanded ed., Birkhäuser, Basel, 2016.Google Scholar
Christensen, O., deFlicht, C., and Lennard, C., Perturbation of frames for a subspace of a Hilbert space. Rocky Mountain J. Math. 30(2000), no. 4, 1237–1249.Google Scholar
Christensen, O. and Hasannasab, M., Frame properties of iterated systems. Appl. Comp. Harm. Anal. 46(2019), 664–673.Google Scholar
Christensen, O., Hasannasab, M., and Philipp, F., Frame properties of operator orbits. Math. Nachr. 293(2020), 52–66.CrossRefGoogle Scholar
Holub, J., Pre-frame operators, Besselian frames and near-Riesz bases. Proc. Amer. Math. Soc. 122(1994), 779–785.CrossRefGoogle Scholar
Marcus, A. W., Spielman, D. A., and Srivastava, N., Interlacing families II: mixed characteristic polynomials and the Kadison–Singer problem. Ann. of Math. (2) 182(2015), no. 1, 327–350.CrossRefGoogle Scholar
Olevskii, V., On orthonormal bases and translates. J. Approx. Theory 202(2016), 1–4.CrossRefGoogle Scholar
Olevskii, V., Completion by perturbations. Preprint, 2020. arXiv:2008.12877Google Scholar
Young, R., An introduction to nonharmonic Fourier series. Academic Press, New York, 1980 (revised first edition 2001).Google Scholar