Article contents
A Coincidence Theorem for Holomorphic Maps to 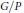 $G/P$
$G/P$
Published online by Cambridge University Press: 20 November 2018
Abstract
The purpose of this note is to extend to an arbitrary generalized Hopf and Calabi-Eckmann manifold the following result of Kalyan Mukherjea: Let 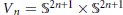 ${{V}_{n}}={{\mathbb{S}}^{2n+1}}\times {{\mathbb{S}}^{2n+1}}$ denote a Calabi-Eckmann manifold. If
${{V}_{n}}={{\mathbb{S}}^{2n+1}}\times {{\mathbb{S}}^{2n+1}}$ denote a Calabi-Eckmann manifold. If 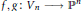 $f,g:\,{{V}_{n}}\to {{\mathbb{P}}^{n}}$ are any two holomorphic maps, at least one of them being non-constant, then there exists a coincidence:
$f,g:\,{{V}_{n}}\to {{\mathbb{P}}^{n}}$ are any two holomorphic maps, at least one of them being non-constant, then there exists a coincidence: 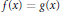 $f(x)\,=\,g(x)$ for some
$f(x)\,=\,g(x)$ for some 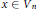 $x\in {{V}_{n}}$ . Our proof involves a coincidence theorem for holomorphic maps to complex projective varieties of the form
$x\in {{V}_{n}}$ . Our proof involves a coincidence theorem for holomorphic maps to complex projective varieties of the form 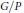 $G/P$ where
$G/P$ where 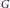 $G$ is complex simple algebraic group and
$G$ is complex simple algebraic group and 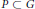 $P\,\subset \,G$ is a maximal parabolic subgroup, where one of the maps is dominant.
$P\,\subset \,G$ is a maximal parabolic subgroup, where one of the maps is dominant.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2003
References
- 3
- Cited by

