Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hermann, Thomas
1992.
On a tolerance problem of parametric curves and surfaces.
Computer Aided Geometric Design,
Vol. 9,
Issue. 2,
p.
109.
Popa, Dorian
and
Raşa, Ioan
2013.
On the stability of some classical operators from approximation theory.
Expositiones Mathematicae,
Vol. 31,
Issue. 3,
p.
205.
Popa, Dorian
and
Raşa, Ioan
2014.
On the best constant in Hyers–Ulam stability of some positive linear operators.
Journal of Mathematical Analysis and Applications,
Vol. 412,
Issue. 1,
p.
103.
Mursaleen, M.
and
Ansari, Khursheed J.
2015.
On the stability of some positive linear operators from approximation theory.
Bulletin of Mathematical Sciences,
Vol. 5,
Issue. 2,
p.
147.
MURSALEEN, M.
ANSARI, Khursheed J.
and
KHAN, Asif
2015.
Stability of some positive linear operators on compact disk.
Acta Mathematica Scientia,
Vol. 35,
Issue. 6,
p.
1492.
Popa, Dorian
Pugna, Georgiana
and
Raşa, Ioan
2016.
Contributions in Mathematics and Engineering.
p.
517.
2018.
Ulam Stability of Operators.
p.
99.
Ait-Haddou, Rachid
Furihata, Daisuke
and
Mazure, Marie-Laurence
2018.
The Hyers–Ulam stability constant for Chebyshevian Bernstein operators.
Journal of Mathematical Analysis and Applications,
Vol. 463,
Issue. 2,
p.
1075.
Ait-Haddou, Rachid
2019.
New stability results for explicit Runge–Kutta methods.
BIT Numerical Mathematics,
Vol. 59,
Issue. 3,
p.
585.
Kaur, Jaspreet
and
Goyal, Meenu
2025.
Hyers-Ulam stability of some positive linear operators.
Studia Universitatis Babes-Bolyai Matematica,
Vol. 70,
Issue. 1,
p.
105.

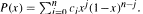 This representation becomes unique if we insist that n equals the degree of
This representation becomes unique if we insist that n equals the degree of