No CrossRef data available.
Article contents
Cockcroft Properties of Thompson’s Group
Published online by Cambridge University Press: 20 November 2018
Abstract
In a study of the word problem for groups, R. J. Thompson considered a certain group 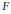 $F$ of self-homeomorphisms of the Cantor set and showed, among other things, that
$F$ of self-homeomorphisms of the Cantor set and showed, among other things, that 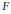 $F$ is finitely presented. Using results of K. S. Brown and R. Geoghegan, M. N. Dyer showed that
$F$ is finitely presented. Using results of K. S. Brown and R. Geoghegan, M. N. Dyer showed that 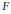 $F$ is the fundamental group of a finite two-complex
$F$ is the fundamental group of a finite two-complex 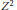 ${{Z}^{2}}$ having Euler characteristic one and which is Cockcroft, in the sense that each map of the two-sphere into
${{Z}^{2}}$ having Euler characteristic one and which is Cockcroft, in the sense that each map of the two-sphere into 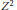 ${{Z}^{2}}$ is homologically trivial. We show that no proper covering complex of
${{Z}^{2}}$ is homologically trivial. We show that no proper covering complex of 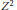 ${{Z}^{2}}$ is Cockcroft. A general result on Cockcroft properties implies that no proper regular covering complex of any finite two-complex with fundamental group
${{Z}^{2}}$ is Cockcroft. A general result on Cockcroft properties implies that no proper regular covering complex of any finite two-complex with fundamental group 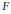 $F$ is Cockcroft.
$F$ is Cockcroft.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000

