Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Kunpeng
and
Zhang, Xianke
2003.
Subgroups of Class Groups of Algebraic Quadratic Function Fields.
Chinese Annals of Mathematics,
Vol. 24,
Issue. 03,
p.
315.
Chakraborty, Kalyan
and
Mukhopadhyay, Anirban
2004.
Exponents of class groups of real quadratic function fields.
Proceedings of the American Mathematical Society,
Vol. 132,
Issue. 7,
p.
1951.
Pacelli, Allison M.
2004.
Abelian subgroups of any order in class groups of global function fields.
Journal of Number Theory,
Vol. 106,
Issue. 1,
p.
26.
Lee, Yoonjin
and
Pacelli, Allison
2005.
Class groups of imaginary function fields: The inert case.
Proceedings of the American Mathematical Society,
Vol. 133,
Issue. 10,
p.
2883.
Chakraborty, Kalyan
and
Mukhopadhyay, Anirban
2005.
Exponents of class groups of real quadratic function fields (II).
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 1,
p.
51.
Pacelli, Allison M.
2006.
The prime at infinity and the rank of the class group in global function fields.
Journal of Number Theory,
Vol. 116,
Issue. 2,
p.
311.
Lee, Yoonjin
and
Pacelli, Allison M.
2006.
Higher rank subgroups in the class groups of imaginary function fields.
Journal of Pure and Applied Algebra,
Vol. 207,
Issue. 1,
p.
51.
Pacelli, Allison M.
2006.
A Lower Bound on the Number of Cyclic Function Fields With Class Number Divisible byn.
Canadian Mathematical Bulletin,
Vol. 49,
Issue. 3,
p.
448.
Bae, Sunghan
2011.
Real quadratic function fields of Richaud-Degert type with ideal class number one.
Proceedings of the American Mathematical Society,
Vol. 140,
Issue. 2,
p.
403.
BANERJEE, PRADIPTO
and
KOTYADA, SRINIVAS
2013.
Divisibility of class numbers of imaginary quadratic function fields by a fixed odd number.
Proceedings - Mathematical Sciences,
Vol. 123,
Issue. 1,
p.
1.
Bae, Sunghan
and
Jung, Hwanyup
2013.
CLASS NUMBER DIVISIBILITY OF QUADRATIC FUNCTION FIELDS IN EVEN CHARACTERISTIC.
Bulletin of the Korean Mathematical Society,
Vol. 50,
Issue. 4,
p.
1357.
Lee, Jungyun
and
Lee, Yoonjin
2016.
Indivisibility of class numbers of real quadratic function fields.
Journal of Pure and Applied Algebra,
Vol. 220,
Issue. 8,
p.
2828.
Ellenberg, Jordan
Venkatesh, Akshay
and
Westerland, Craig
2016.
Homological stability for Hurwitz spaces and the Cohen-Lenstra conjecture over function fields.
Annals of Mathematics,
Vol. 183,
Issue. 3,
p.
729.

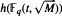 denote the ideal class number of the real quadratic function field obtained by adjoining the square root of an even-degree monic
denote the ideal class number of the real quadratic function field obtained by adjoining the square root of an even-degree monic 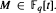 . The following theorem is proved: Let n ≧ 1 be an integer not divisible by
. The following theorem is proved: Let n ≧ 1 be an integer not divisible by 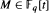 such that
such that 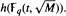 . The proof constructs an element of order
. The proof constructs an element of order 