Article contents
Characterizations of Axiomatic Categories of Models Canonically Isomorphic to (Quasi-)Varieties
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 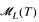 be the category of all homomorphisms (i.e. functions preserving satisfaction of atomic formulas) between models of a set of sentences T in a finitary first-order language L. Functors between two such categories are said to be canonical if they commute with the forgetful functors. The following properties are characterized syntactically and also in terms of closure of
be the category of all homomorphisms (i.e. functions preserving satisfaction of atomic formulas) between models of a set of sentences T in a finitary first-order language L. Functors between two such categories are said to be canonical if they commute with the forgetful functors. The following properties are characterized syntactically and also in terms of closure of 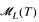 for some algebraic constructions (involving products, equalizers, factorizations and kernel pairs): There is a canonical isomorphism from
for some algebraic constructions (involving products, equalizers, factorizations and kernel pairs): There is a canonical isomorphism from 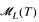 to a variety (resp. quasivariety) in a finitary expansion of L which assigns to a model its (unique) expansion. This solves a problem of H. Volger.
to a variety (resp. quasivariety) in a finitary expansion of L which assigns to a model its (unique) expansion. This solves a problem of H. Volger.
In the case of a purely algebraic language, the properties are equivalent to:“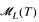 is canonically isomorphic to a finitary variety (resp. quasivariety)” and, for the variety case, to “the forgetful functor of
is canonically isomorphic to a finitary variety (resp. quasivariety)” and, for the variety case, to “the forgetful functor of 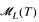 is monadic (tripleable)”.
is monadic (tripleable)”.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1988
References
- 4
- Cited by

