Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-12T02:02:33.954Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of the Lebesgue Integral

Published online by Cambridge University Press:  20 November 2018

B. S. Thomson
B. S. Thomson*
Affiliation:
Dept. of Maths, Simon Fraser University, Burnaby, B.C. , CanadaV5A 1S6
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The first general integrability criterion is due to Riemann. He observed that a necessary and sufficient condition for a function f(x) on [a, b] to be integrable in his sense is that for each ε > 0 there exists a δ > 0 so that

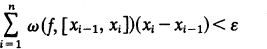
where {x0, x1, …, xn} is a partition of [a, b] with diameter less than δ (and ω(f, I) denotes the oscillation of f on the interval I).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 20 , Issue 3 , 01 September 1977 , pp. 353 - 357
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Henstock, R., The equivalence of generalized forms of the Ward, variational, Denjoy-Stieltjes and Perron-Stieltjes integrals, Proc. London Math. Soc. (3), 10 (1960), pp. 281-303.Google Scholar
2. Henstock, R., A Riemann-type integral of Lebesgue power, Canad. J. Math. 20 (1968), pp. 79-87.Google Scholar
3. McShane, E. J., A Riemann-type integral that includes Lebesgue-Stieltjes, Bochner and Stochastic integrals, Memoirs of the Amer. Math. Soc. No. 88, 1969.Google Scholar
4. McShane, E. J., A unified theory of integration, Amer. Math Monthly, (80) no. 4 (1973), pp. 349-359.Google Scholar
5. Saks, S., Theory of the Integral, 2nd English edn. (Warsaw, 1937).Google Scholar
6. Thomson, B. S., A theory of integration, Duke Math J., vol. 39 (1972), pp. 503-510.Google Scholar