Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Al-Salam, Waleed
Allaway, W. R.
and
Askey, Richard
1984.
Sieved ultraspherical polynomials.
Transactions of the American Mathematical Society,
Vol. 284,
Issue. 1,
p.
39.
Desesa, Blaise
1998.
Orthogonality of Sieved Random Walk Polynomials from a Nonsieved Analogue.
SIAM Journal on Mathematical Analysis,
Vol. 29,
Issue. 1,
p.
251.
Odake, Satoru
and
Sasaki, Ryu
2015.
Reflectionless potentials for difference Schrödinger equations.
Journal of Physics A: Mathematical and Theoretical,
Vol. 48,
Issue. 11,
p.
115204.
Odake, Satoru
and
Sasaki, Ryu
2015.
Solvable discrete quantum mechanics: q-orthogonal polynomials with q=1 and quantum dilogarithm.
Journal of Mathematical Physics,
Vol. 56,
Issue. 7,

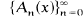 that can be represented as
that can be represented as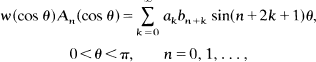
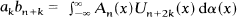 when
when 